База данных по теплофизическим свойствам жидкометаллических теплоносителей перспективных ядерных реакторов
Теплофизические свойства жидкого cвинца и эвтектического сплава свинца и висмута
ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОМЕТАЛЛИЧЕСКИХ ТЕПЛОНОСИТЕЛЕЙ
Раздел составлен по работам [17, 18, 19, 20, 21, 32, 43, 44, 47÷49], большая часть текста заимствована из [18].
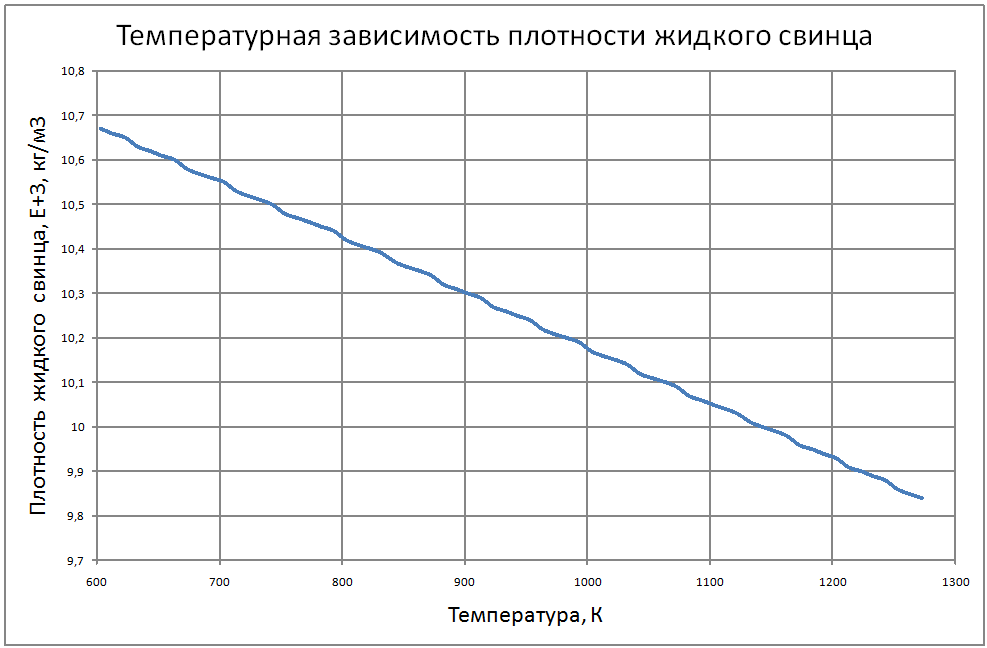
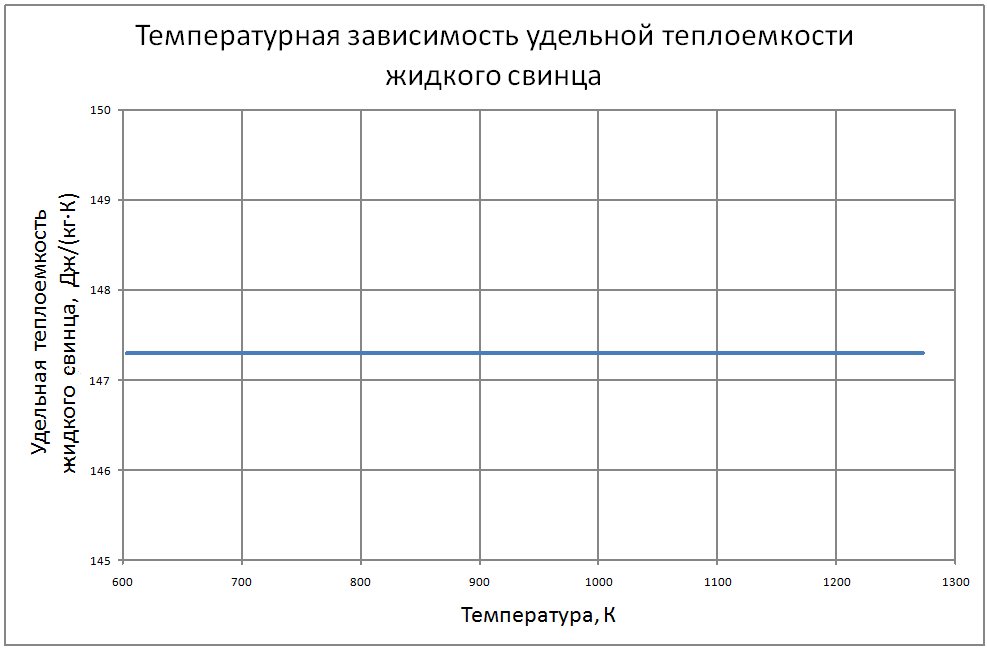
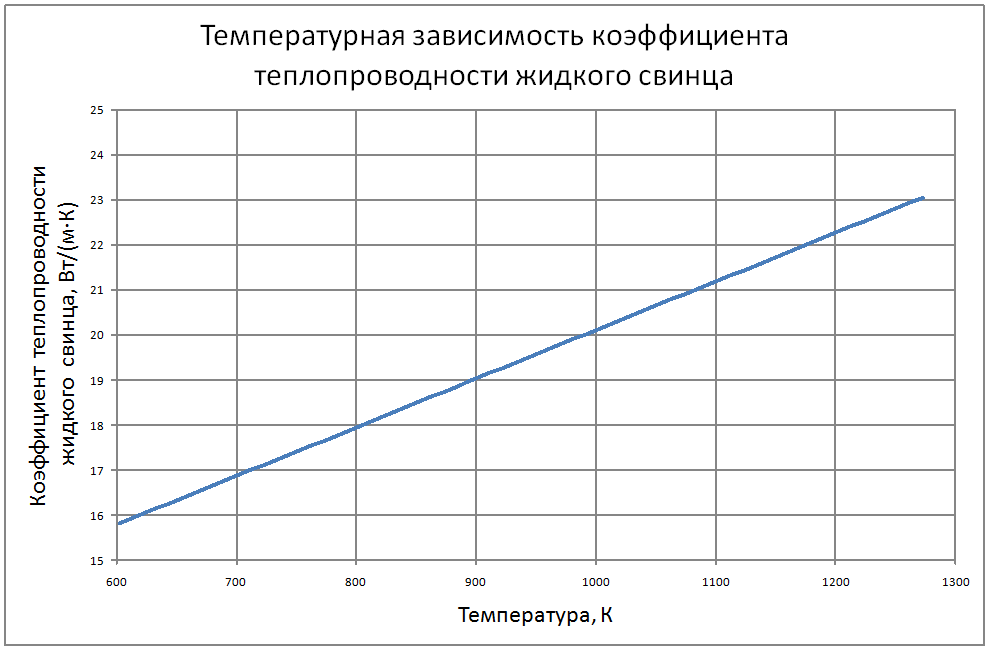
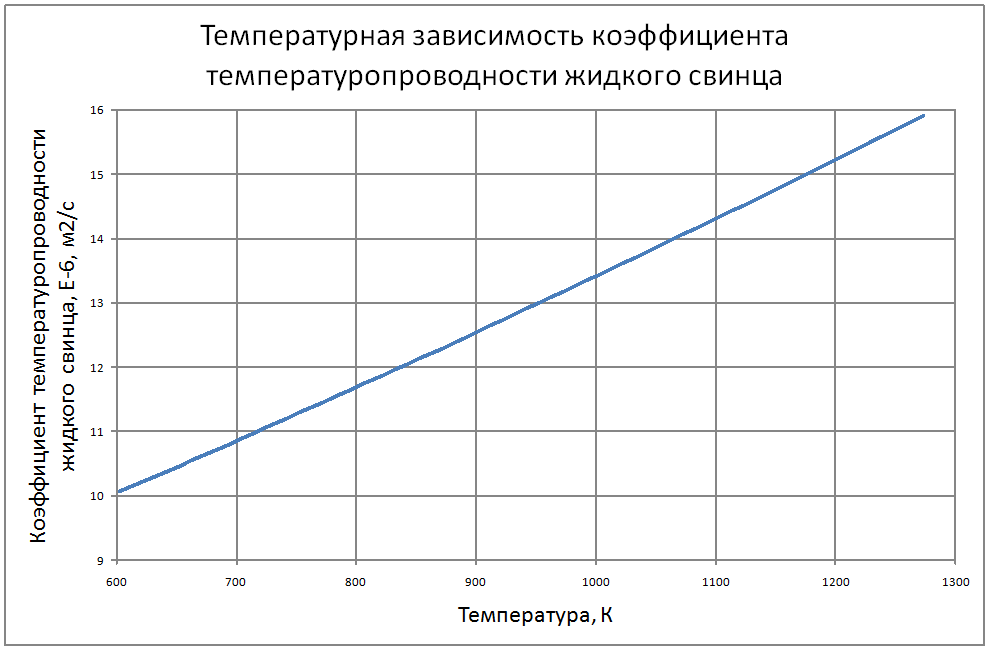
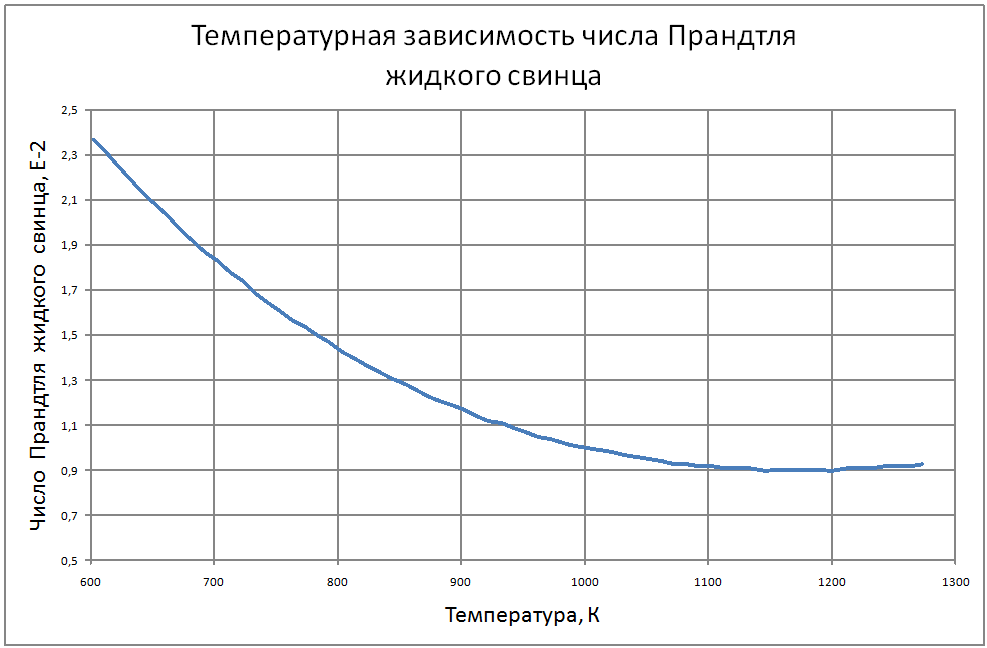
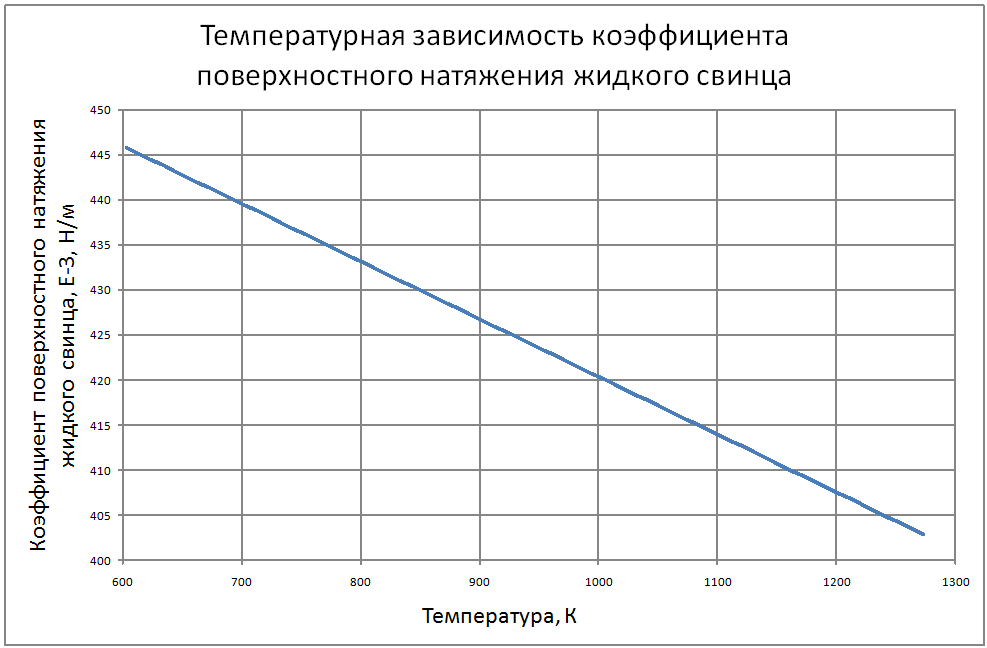
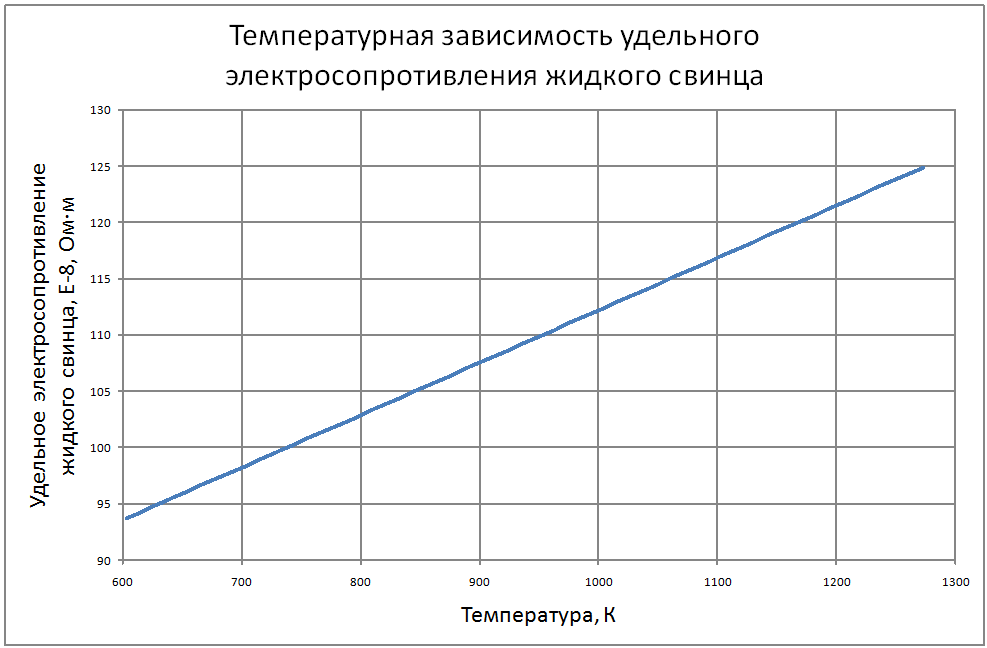
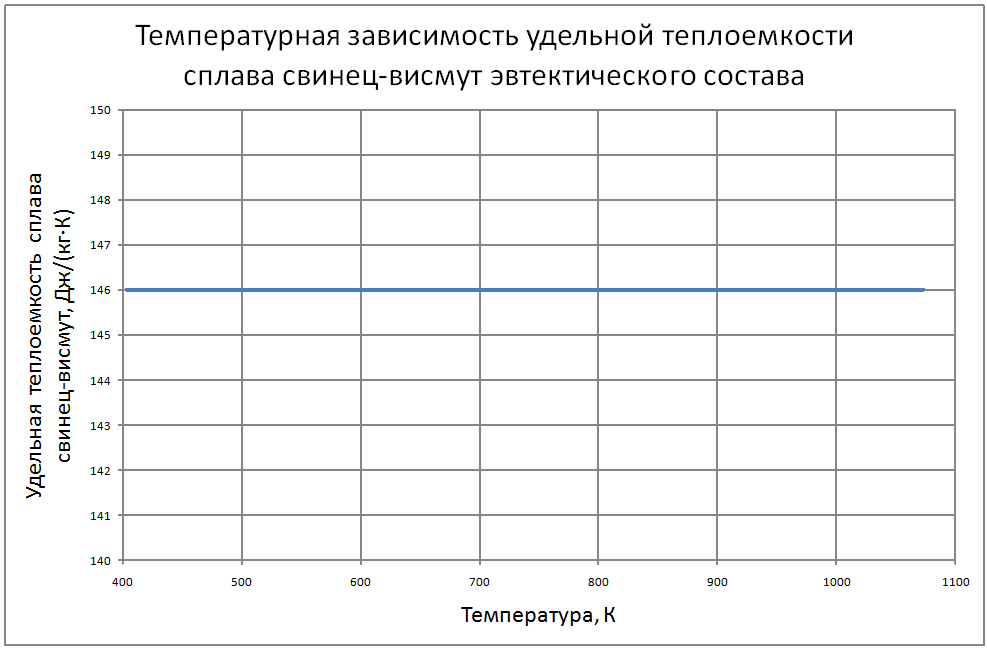
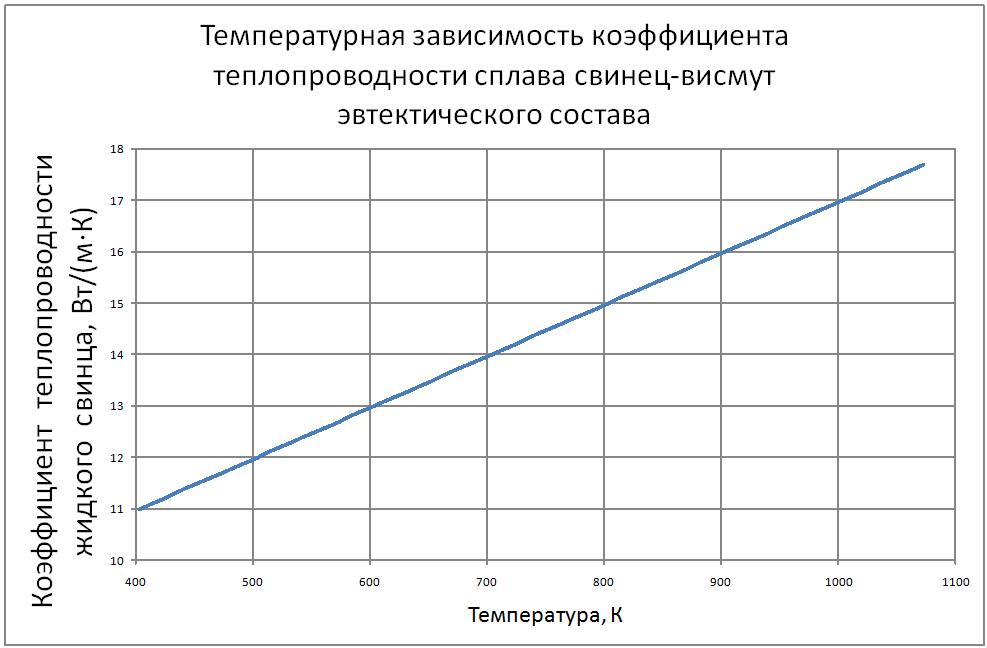
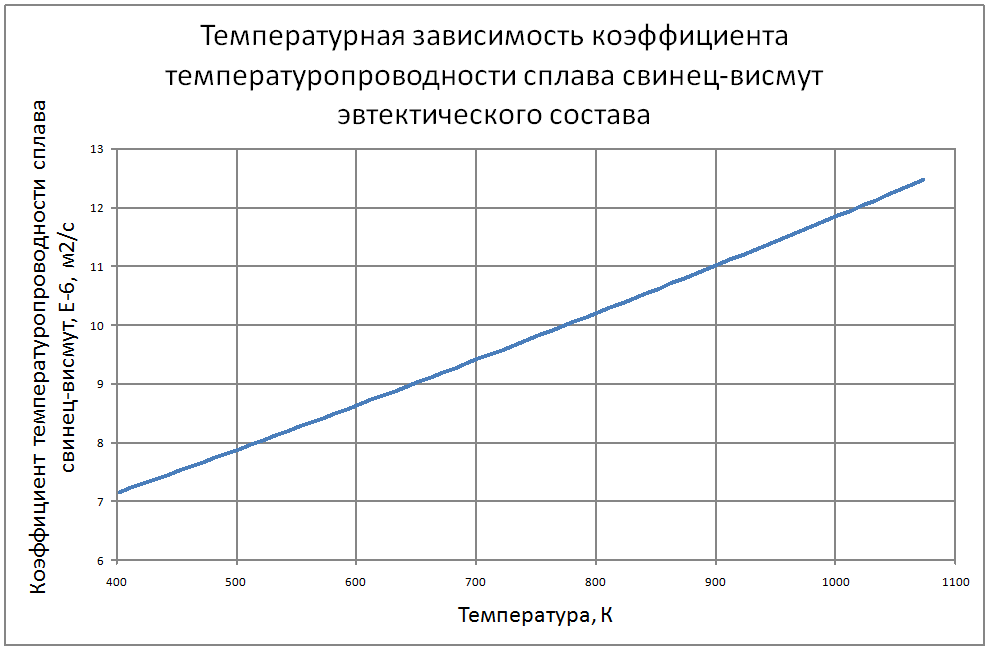
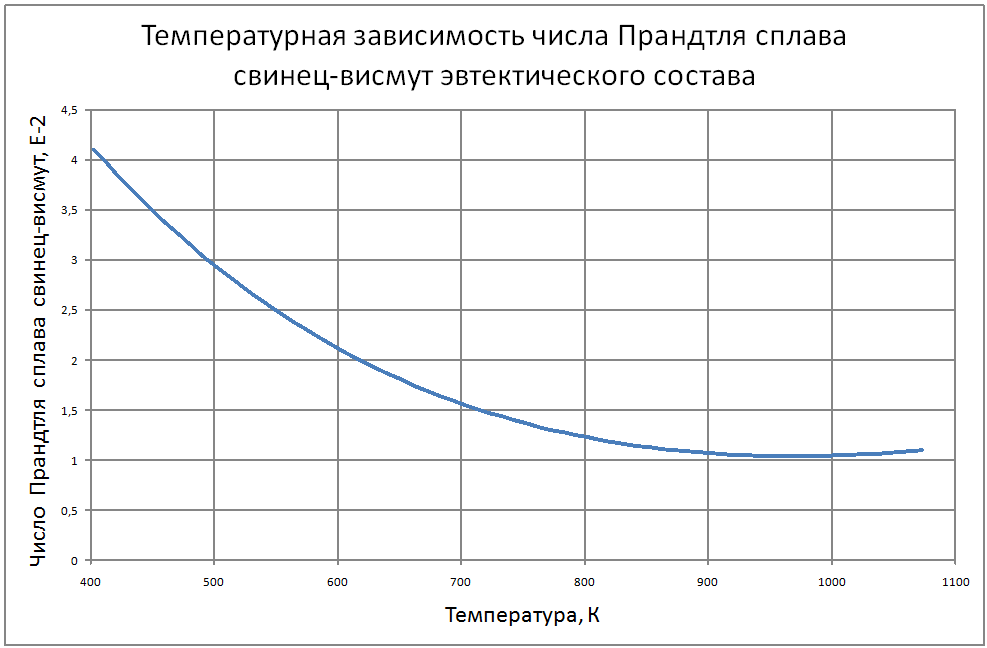
Далее соотношения даны в следующих единицах: T в К; t в °C; ρ в кг/м3; Сp в Дж/(кг·К); λ в Вт/(м·К); a в м2/с; ν в м2/с ; σ в Н/м; ρе в Ом·м. Погрешности показаны в конце раздела. Плотность свинца Для расчетов рекомендуется аппроксимационная формула кг/ м3: ρ = [(11,42±0,01) -(12,42±0,12)10–4T ] ·103 (1) Плотность сплава свинец-висмут Плотность сплава свинец-висмут эвтектического состава (Pb -45.4%, Bi - 55.4% по массе) рассчитана по закону аддитивности и может быть аппроксимирована формулой. кг/ м3 : ρ = [(11,05±0,01) –(12,49±0,12)·10–4T]·103 (2) Теплоемкость сплава свинец-висмут В справочном материале по теплофизическим свойствам расплавленных материалов, подготовленном группой специалистов ЭНИН Никольским и др. [18], даются следующие значения теплоемкостей: Висмут 0,036 ккал/(кг·К) = 150,6 Дж/(кг·К) Свинец 0,0352 ккал/(кг·К) = 147,3 Дж/(кг·К) Эвтектический сплав 147,3 Дж/(кг·К), Если воспользоваться законом аддитивности, то из этих данных для сплава должно быть значение 149,1 Дж/(кг·К), Анализ данных по теплопроводности методами статистики невозможен из-за отсутствия информации в оригинальных работах. В [18] обобщения сделаны на основе сравнения результатов различных авторов с теоретической зависимостью таплопроводности от температуры (λ(Т) = L0T/ρe(T)), которая следует из закона Видемана-Франца при использовании теоретического значения числа Лоренца (L0 = 2.443·10-8 Вт·Ом/K2). Здесь ρe(T)-удельное электросопротивление жидкого металла при температуре Т. Среднее значение теплопроводности, полученное статистической обработкой результатов около температуры кристаллизации авторы [18] оценивают значением 15,8 ±1,3 Вт/(м·К) и для использования рекомендуют соотношение Пауэлла [3]: λ = 15,8 + 108·10-4 (Т-600,4), Вт/(м·К) (3) Экстраполяция этого соотношения на область высоких температур дает хорошее согласие в пределах экспериментальных погрешностей с данными Банчилла, Филиппова [17]. Первые измерения теплопроводности сплава PbBi были выполнены Брауном, Биениасом в 20-х годах. Позже были опубликованы справочные таблицы специалистов ЭНИН - Никольский и др. и измерения Кржижановского (теплопроводность и электрическое сопротивление). Учитывая близость атомных весов компонентов сплава, их процентных долей по массе и объемных долей (Pb-0,491, Bi-0,509) можно сделать оправданные оценки теплопроводности по закону аддитивности. Другие расчетные оценки были выполнены Кирилловым в соответствии с теорией Одолевского и предложения Новикова. Наиболее надежными по [18] являются совпадающие данные, которые могут быть аппроксимированы формулой: λ = 11+9,9·10-3 (Т-397)(4) Аппроксимирующая формула для коэффициента кинематической вязкости свинца из справочных данных для t = 400-700 °С, представленных в [3, 17], имеет вид: ν = (43,8–7,57·10–2 t+0,467·10–4 t)210–8±1,2% (5) Однако, она дает неверные результаты при экстраполяции на более высокие температуры (>800°С). Более предпочтительна формула, которая получена из обработки тех же данных [3, 17] в других координатах: ν = [15,87·103/T-2,65]10–8,(6) где Т в [K], ν в м2/c. Для сплавов свинца с висмутом, по своим термодинамическим свойствам близким к идеальным, предложено большое количество формул, связывающих вязкость сплава, состав его и вязкость компонентов. Эти зависимости представлены формулой: f(μ) = ∑Ni f(μi)(7) на месте f(μ) могут стоять μ, ν, 1/μ, 1/ν, lgμ, lgν, на месте f(μi) соответствующие вязкости компонентов, Ni -молярные или объемные доли. Эти выражения носят эмпирический характер. Аддитивность μ наблюдалась во многих сплавах, где теплота смешения (ΔH) компонентов мала и свойства компонентов близки: μ = (N1μ1 + N2μ2)(1-2ΔH/RT) (8) Справочные данные[3, 17] аппроксимируются зависимостью: ν· = [68,9-0,126Т+6,95·10-5 Т2] 10-8 (9) Однако, если справедлив для кинематической вязкости закон аддитивности, то формула должна иметь вид: ν· = 10-8[12,88·103/T-1,89](10) Пока причины расхождений значений, получаемых по формулам (9) и (10) не выяснены, рекомендуется использовать формулу (8) Зависимость поверхностного натяжения от температуры веществ, для диапазона температур вдалеке от критической точки, является линейной σ = σm-dσ/dT(T-Tm) где σm , Tm - поверхностное натяжение и температура в точке плавления. Значения σm, dσ/dT по данным справочника Ниженко и др. [23] для Pb и Bi находятся в следующих пределах: свинец σm = 410÷470 Н/м; висмут σm = 360÷390 Н/м; Поверхностное натяжение чувствительно к наличию примесей в жидкости и паре. При отборе данных использовались сведения последних публикаций [23]. σ(Pb) = 446 – 0,0640(T - 600)(11) σ(Bi) = 375 – 0,0766(T - 545)(12) Близость поверхностных натяжений чистых компонентов позволяет использовать правило аддитивности для вычисления σ (сплава PbBi): σ(PbBi) = 416 – 0,0703(T - 398) (13) Этот результат подтверждается прямыми измерениями в [23]. Удельное электрическое сопротивление Температурная зависимость ρe (удельное электрическое сопротивление) жидкого свинца линейна. На основании анализа ряда работ и своих собственных измерений авторы обзора [20] обобщили результаты для интервала температур 600÷1200 К соотношением: ρe = [(65,73 ± 0,15) + (4,65 ± 0,05)·10-2T]10-8(14) Для температур 1100 - 2400 К можно воспользоваться формулой из работы [17] ρe = [-84,5 + 0,3655T – 2,135·10-4T2 + 4,77·10-8T3] 10-8(15) Результаты обобщения [18] по удельному сопротивлению висмута описываются формулой: ρe = [(97,45±0,8) + (5,70 ± 0,12)·10–2T] 10-8 (16) Удельное электрическое сопротивление сплава свинца с висмутом Используя закон аддитивности из формул (14)÷(16), получим: ρe = [(83,3 ± 0,5) + (5,23 ± 0,09)·10-2T] 10-8 (17) Экспериментальные данные практически совпадают со значениями, вычисленными по этой формуле. Давление насыщенных паров В монографии Несмеянова [24] рекомендуется соотношение: lgP(мм.рт.ст.) = А–В/Т+СТ+DlgT. Исследования показали, что в парах Bi находится значительное количество двухатомных молекул Bi2, доля которых при 6000 ~ 40%, при 9000 ~ 20%. При измерении температуры происходит и изменение состава пара. Приближенные соотношения (±10%) для давлений насыщенных паров имеют вид. Давление насыщенных паров для свинца: при T<1000 K lgP(Па) = 10,0–9840/T(18) T>1000 K lgP(Па) = 9,844–9804/T(19) Давление насыщенных паров для висмута: при T<1000 K lgP(Па) = 10,57–9014/T (20) Используя зависимости, вытекающие из закона Рауля, можно вычислить давление пара над сплавом (Р) Р = PPb NPb+РBiNBi(21) где РPb, РBi - давление насыщенного пара над чистыми компонентами; NPb, NBi - мольные доли компонентов в сплаве - (NPb = 0,553; NBi = 0,447). Проведенный в [18] анализ теплофизических свойств свинца и сплава свинец-висмут эвтектического состава показал достаточно удовлетворительную точность описания по отношению к экспериментальным данным по следующим свойствам: - плотность - (± 0,2%) - теплоемкость - (± 0,2%) - вязкость - (± 1,5%). Расходятся данные разных исследователей по: - теплопроводности - (± 15%) - поверхностному натяжению - (± 15%) - давлению паров элементов - (± 10%). В таблицах ниже представлены сводные данные о теплофизических свойствах свинца и эвтектического сплава свинец-висмут. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||