База данных по теплофизическим свойствам газов и их смесей, используемых в ЯЭУ
Теплофизические свойства смеси инертных газов
ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ГАЗОВ В ЯЭУ
Соотношения для расчета характеристик
чистых компонентов гелия He, криптона Kr, и ксенона Xe в рассматриваемом
диапазоне температур и давлений показаны в предыдущих разделах.
Термодинамические характеристики всех трех газов в первом приближении можно
описать уравнением состояния идеального газа pv = RT с малыми поправками
на парные (и тройные для ксенона Xe) взаимодействия.
Транспортные свойства, т.е. коэффициент динамической вязкости, теплопроводности
и т.д. можно описать, используя молекулярно-кинетическую теорию разреженных
газов для парных межатомных взаимодействий. При этом необходимо учитывать тройные
столкновения, которые определяют первые плотностные поправки к кинетическим
коэффициентам. Эти представления можно применить и к
смесям рассматриваемых газов. Анализ теплофизических характеристик
неплотных смесей инертных газов при высоких температурах проведен в работе
[25], где обобщение данных о втором вириальном и кинетических коэффициентах
выполнено одновременно для всех чистых инертных газов и их смесей по принципу
собственных состояний. В работе [26] разнородные экспериментальные данные для
чистых инертных газов и их смесей были взяты за основу для восстановления шести
параметрических потенциалов парных взаимодействия U(r). Получено удовлетворительное согласование основных массивов
экспериментальных данных и справочных значений [26], полученных по результатам,
приведенным в работе [22]. Основным аргументом для обоснования достоверности
разработанных рекомендаций можно считать согласованность характеристик,
проведенную на основе теоретических моделей для потенциалов взаимодействий, и
полуэмпирических моделей для принципа соответственных состояний. Приведенные ниже корреляции
используют соотношения молекулярно-кинетической теории разреженных и неплотных
газов и газовых смесей, приведенные в работе [22]. Обобщение зависимостей
второго вириального коэффициента и интегралов столкновения проведено на основе
соотношений, приведенных в работе [25]. Расчеты проводились с учетом высоких
температур. Удельный объем, плотность Удельный объем (на единицу массы
смеси), м3/кг, [22]:
где R = R*/M
- удельная газовая постоянная, R* = 8314,51 ± 0,14 Дж/(моль·K) - универсальная газовая постоянная.
M - молекулярный вес смеси
компонентов, Xi - мольные доли компонентов, Mi - мольные
веса компонентов, таблица ниже.
значения dij,
eij и ai приведены в таблицах ниже. Удельная изобарная теплоемкость Удельная изобарная теплоемкость, Дж/(кг·K), [13]:
где давление P в Пa, температура T в K, R и B приведены выше.
Погрешность определяется погрешностью для R, погрешностью заданных мольных
долей смеси и погрешностью теплоемкостей составляющих смеси. Удельная изохорная теплоемкость Удельная изохорная теплоемкость, Дж/(кг·K), [15]:
где давление P в Пa,
температура Т в К, R и B приведены выше. Погрешность
рассчитывается, как сказано ранее. Показатель адиабаты (изоэнтропы) Показатель изоэнтропы,
[13]:
где давление P измеряется в Пa, V - в м3/кг. Скорость звука Скорость звука, м/с,
[13]:
Удельная энтальпия Удельная энтальпия, Дж/кг, [13]:
где давление P в Пa,
температура Т в К, R и B приведены выше. Погрешность
меньше 0,5 % при точном задании
состава смеси. Удельная энтропия Удельная энтропия, Дж/(кг·K), [15, 26]:
где давление P измерено в Пa,
температура Т - в К, R и B показаны выше, Sio по таблице ниже. Погрешность менее
0,5 % при точном задании состава смеси. Коэффициент динамической вязкости Коэффициент динамической вязкости, Па·с, [22, 9]:
Для вязкости смеси в разреженном
состоянии βo(T, x) имеется строгое решение, но оно приводит к
сложным соотношениям. Рекомендуется ограничиться более простым соотношением:
где
Плотностная поправка в (2.8.15):
где
где bio по формуле (6), T*i=T/ei, рассчитаны
по формулам (5) и (6) для значений bi и ei. Величина погрешности
определения β смеси при
T = 300 ÷ 1500 К менее 2,5 %, а при
T = 1500 ÷ 2500 К не превышает 4 %. Коэффициент теплопроводности Коэффициент теплопроводности, Вт/(м·K). При расчете коэффициента
теплопроводности применено простое соотношение:
где
где φij рассчитаны по формуле
(17),
Поправка на плотность рассчитывается
по формуле:
где
Значения ci в (5), показаны в таблице ниже.
Погрешность определения α смеси при температуре в диапазоне
T = 300
- 1500 К
не превышает 2 %, а при температуре в диапазоне T = 1500 - 2500 К не превышает
3 %.
Прочие характеристики Соотношение δ = β/r используется для расчета коэффициента кинематической
вязкости; γ = α/(Hpr) – для коэффициента температуропроводности, и ε = δ/γ – для числа Прандтля. |
|||||||||||||||||||||
Атомные веса элементов приведены по работам [10, 11]. Величины энтропии So элементов в стандартном газовом состоянии при Т = 300 К определены по работе [10]. |
|||||||||||||||||||||
|
|||||||||||||||||||||
|
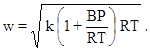 (12)
(12)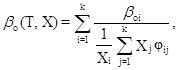 (16)
(16)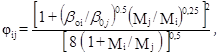 (17)
(17)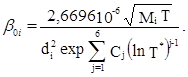 (18)
(18)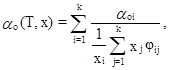 (22)
(22)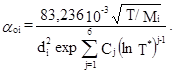 (23)
(23)