База данных по теплофизическим свойствам жидкометаллических теплоносителей перспективных ядерных реакторов
Теплофизические свойства жидкого натрия и его пара
ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОМЕТАЛЛИЧЕСКИХ ТЕПЛОНОСИТЕЛЕЙ
Натрий является одним из наиболее освоенных щелочных металлов, нашедшим широкое применение в различных областях промышленности, особенно в ядерной энергетике. Исследованию свойств жидкометаллических теплоносителей посвящено большое количество работ, настолько большое, что на страницах данного справочника не представляется возможности поместить весь этот список. Да в этом и нет большой необходимости по той причине, что имеется в наличии ряд работ, обобщающих эти материалы [1÷10]. Использовались, в основном, эти работами, хотя пришлось ряд рекомендаций уточнить по первоисточникам. Основная цель данной работы дать достоверную информацию для расчета приведенных здесь свойств с указанием возможной погрешности и пределов применения. Приводятся как аналитические соотношения для описания и расчета свойств, так и таблицы свойств в самом широком диапазоне параметров (температуры). В ряде случаев приходилось приводить разные формулы для разных диапазонов параметров. Это было необходимо потому, что ряд свойств имеют необычайно сложные зависимости. В некоторых случаях невозможно было восстановить значения погрешностей. В этих случаях приводились оценки погрешностей по аналогии с другими веществами. Все приведенные табличные данные проверены по данным в указанной литературе, а формулы проверены расчетом по изготовленным авторами программам. Натрий – химический элемент первой группы с атомным номером 11 в Периодической системе элементов, при нормальных условиях – серебристо-белый металл, в тонких слоях с фиолетовым оттенком, пластичен, даже мягок (легко режется ножом), свежий срез натрия блестит. Металлический натрий был впервые получен в 1807 году Г. Дэви. Природный натрий состоит практически из одного нерадиоактивного изотопа 23Na. Содержание натрия в земной коре составляет 2,64% по массе, в гидросфере натрий содержится в виде растворимых солей в количестве около 2,9%, содержание натрия в морской воде 10500 мг/л (абсолютное содержание составляет 1,5⋅1016 т). В природе натрий находится только в виде солей. Важнейшие минералы натрия: галит (каменная соль) NaCl; мирабилит (глауберова соль) Na2SO4⋅10H2O; тенардит Na2SO4; чилийская селитра NaNO3; криолит Na3[AlF6], трона NaHCO3⋅NaCO3⋅2H2O; бура (тинкал) Na2B4O7⋅10H2O; природные силикаты - альбит Na [AlSiO3O8] и нефелин Na[AlSiO4]. Раздел составлен по материалам работ [1÷8].
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
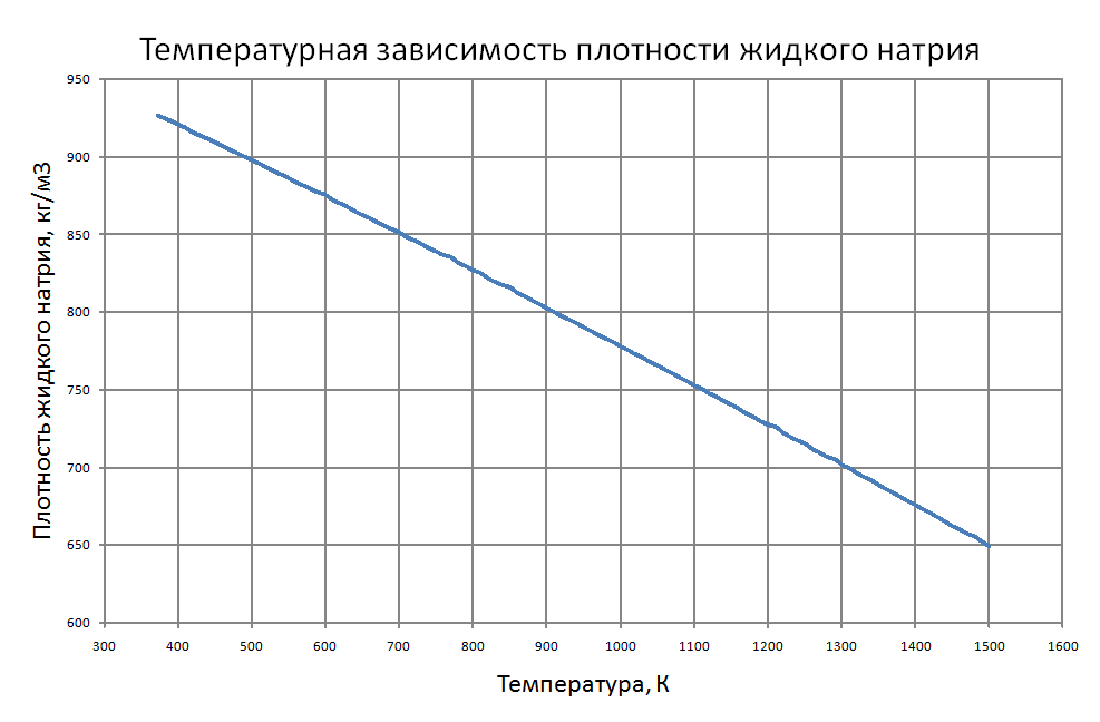
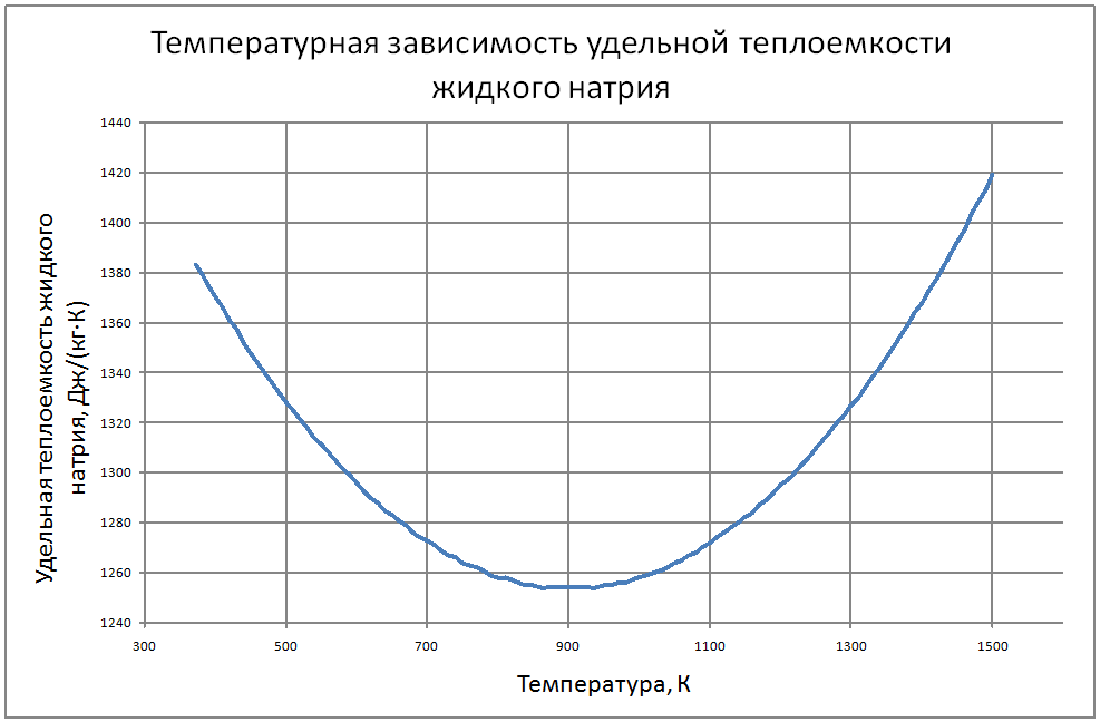
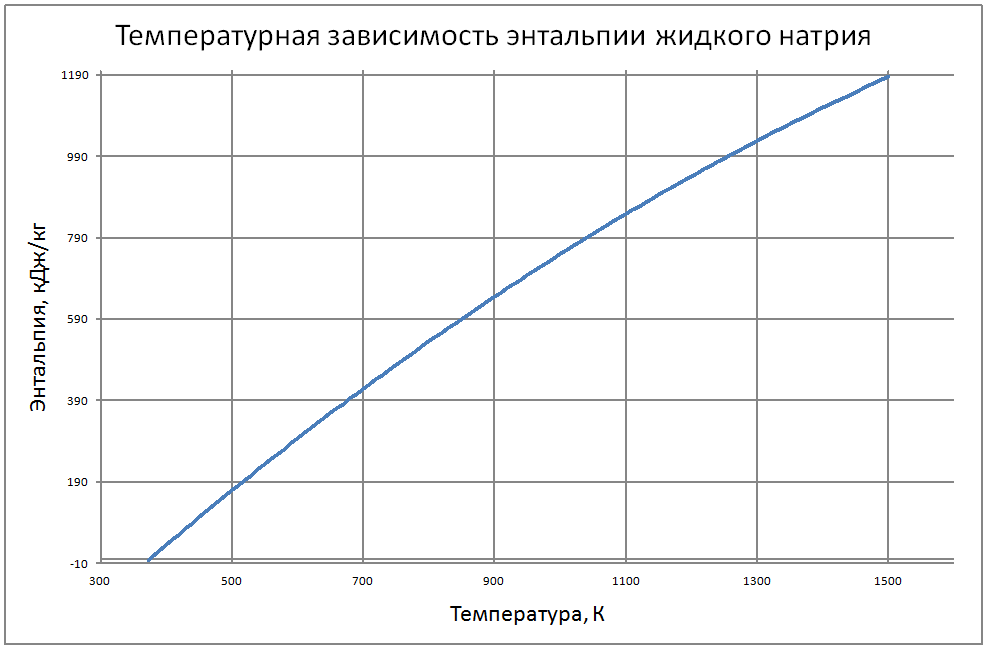
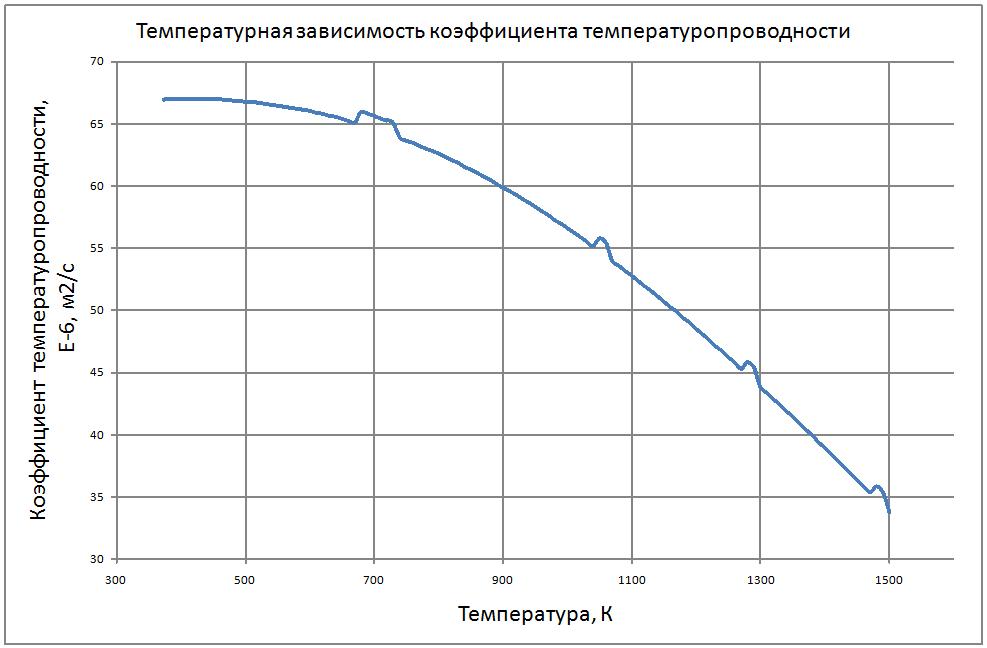
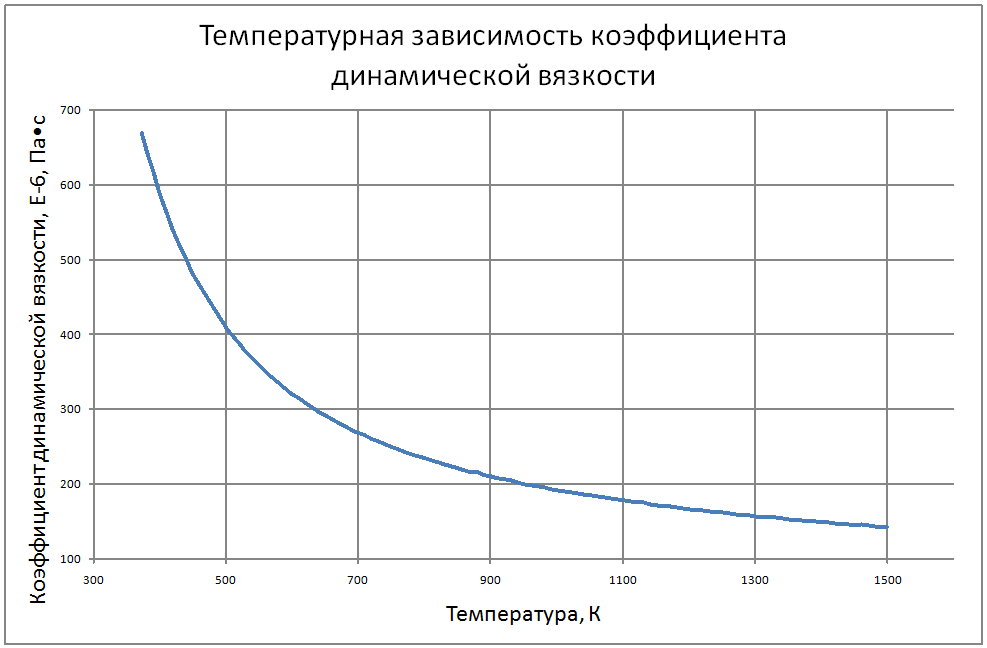
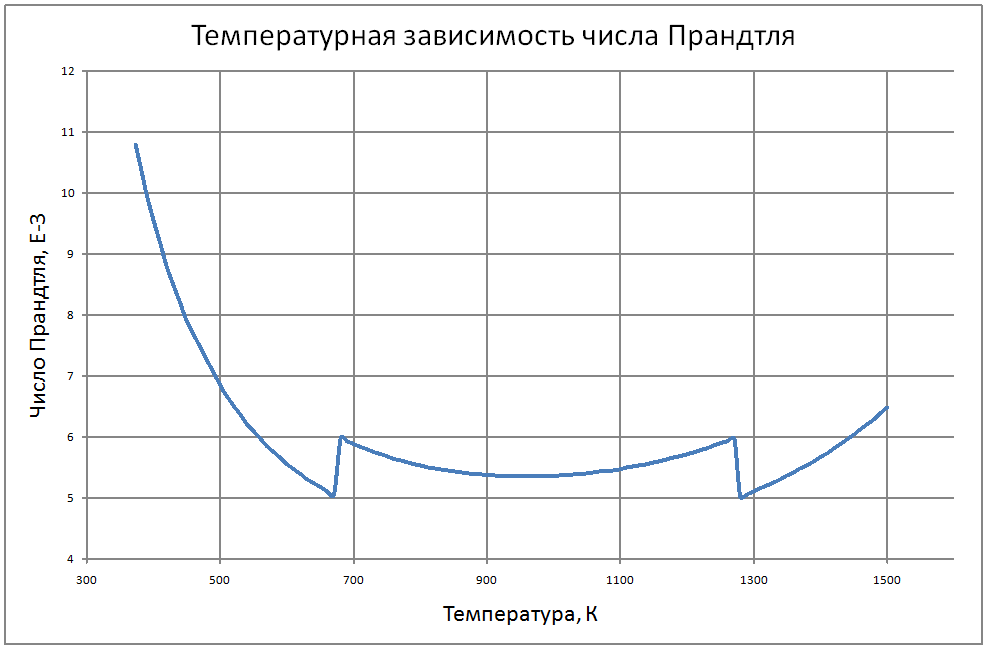
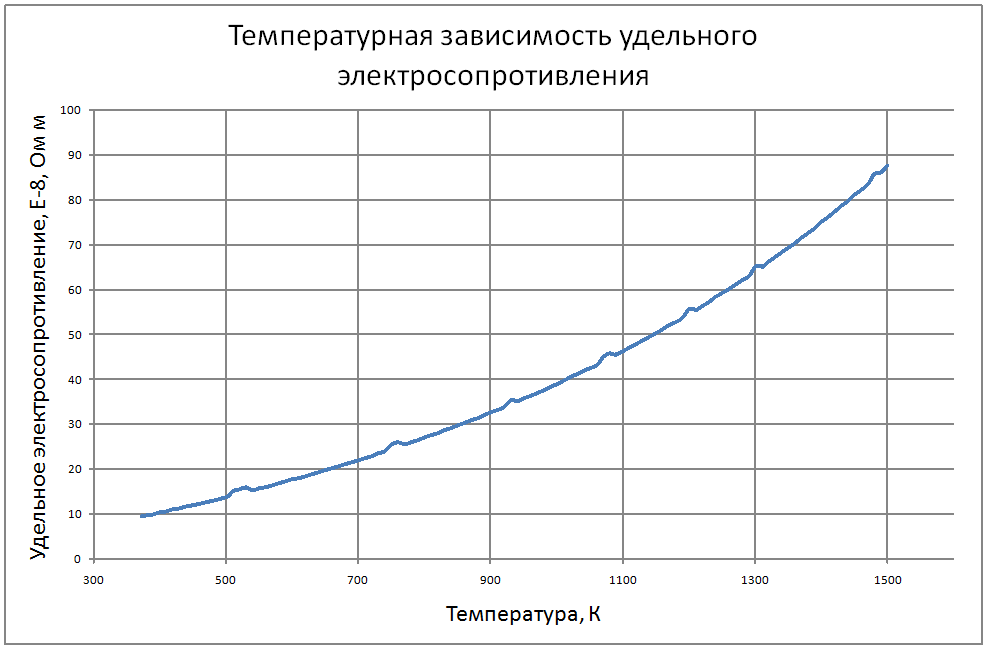
Здесь приведены теплофизические свойства натрия до температуры кипения при атмосферном давлении. Плотность жидкого натрия рассчитывается по формуле: ρ = 949-0,223t-1,75·10-5 t2, (1) где r в кг/м3, t в °С. Пределы применимости формулы: t = 100÷1200 °С. Погрешность Δ расчета ρ составляет ± 0,3 %. Удельная теплоемкость жидкого натрия рассчитывается по формуле: Cр = 1436-0,5805 t+4,62·10-4 t2, (2) где C в Дж/(кг•С); t в °С. Пределы применимости формулы: t = 100÷1200 °С. - при t = 100÷800 °С составляет ± 1 %. - при t = 800 ÷ 1200 °С составляет ± 3 %. Энтальпия (интеграл от соотношения (2)): H(t)-H(t = 100) = -140954+1437t-0,29t2+1,54•10-4t3, (3) где H в Дж/кг, t в °С. Коэффициент теплопроводности жидкого натрия рассчитывается по формуле: λ = 90,6-0,04852t, (4) где λ в Вт/(м•С); t в °С. Пределы применимости формулы: t = 100÷1200 °С. Погрешность Δ расчета λ составляет ± 3 % Коэффициент температуропроводности жидкого натрия рассчитывается по формуле: a = 10-5 (6,6951 + 5,264·10-4 t-2,689·10- 6· t2), (5) где а в м2/с; t в °С. Пределы применимости формулы: t = 100÷1200 °С. Погрешность Δ расчета а: - при t = 100÷800 °С составляет ± 0,5 %. - при t = 800÷1200 °C составляет ±1 %. Коэффициент динамической вязкости жидкого натрия рассчитывается по формуле: μ = 1,2162·10-5ρ1/3 exp(0,6976 ρ/T),(6) где μ в Па·с, T в K. Пределы применимости формулы: T = 300÷1500 °С. Погрешность Δ расчета μ составляет ± 3 %. Кинематическая вязкость и число Прандтля рассчитываются по соотношениям: v = μ/ρ, Pr = v/a, (7) Коэффициент поверхностного натяжения жидкого натрия рассчитывается по формуле: σ = 10-3(247-142,3 10-3 Т+50,33 106Т2-16,62 10-9Т3), (8) где σ в Н/м; T в °K. Пределы применимости формулы: T = 400 ÷ 1200 °K. Погрешность Δ расчета σсоставляет ± 8 %. Давление пара на линии насыщения рассчитывается по формуле: Ps = 10M, (9) M = lnPs = -2,495·ln(T/1000)-13,291· (T/1000)-1 +7,844+1,71· (T/1000) -0,172· (T/1000)2-0,0088· (T/1000)3-0,0091· (T/1000)4+0,0029· (T/1000)5, P в МПа Пределы применимости формулы: t = 300 ÷ 1500 °С. Удельное электросопротивление рассчитывается по формуле: ρe = 10-8 [4,905 ·109 T-1-2,777 ·106+0,433· 103T]-1, Ом·м.(10) Пределы применимости формулы (10) t = 300 ÷ 1500 °С. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
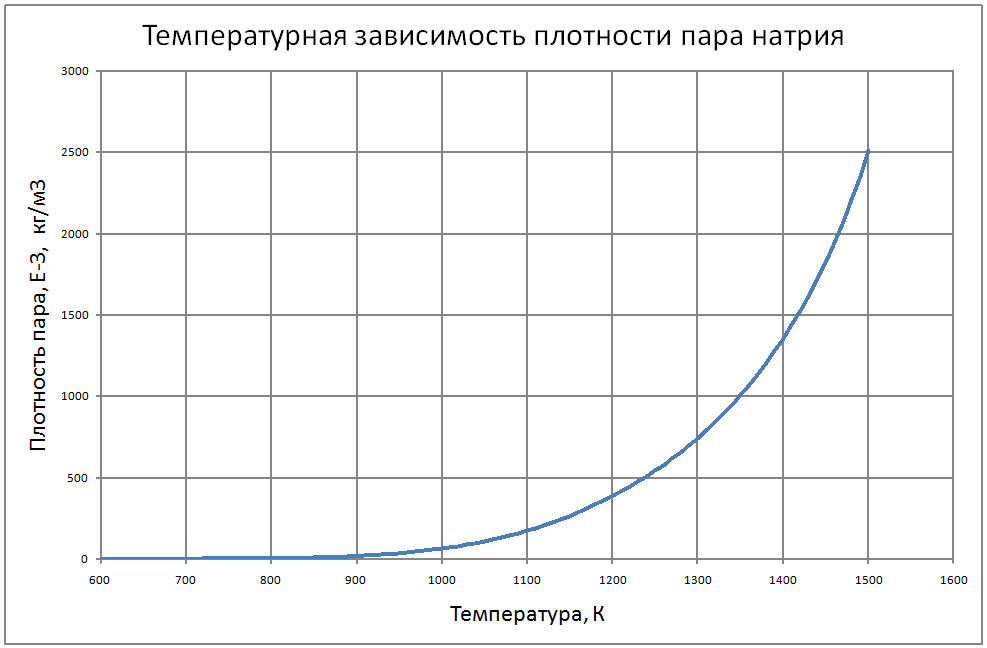
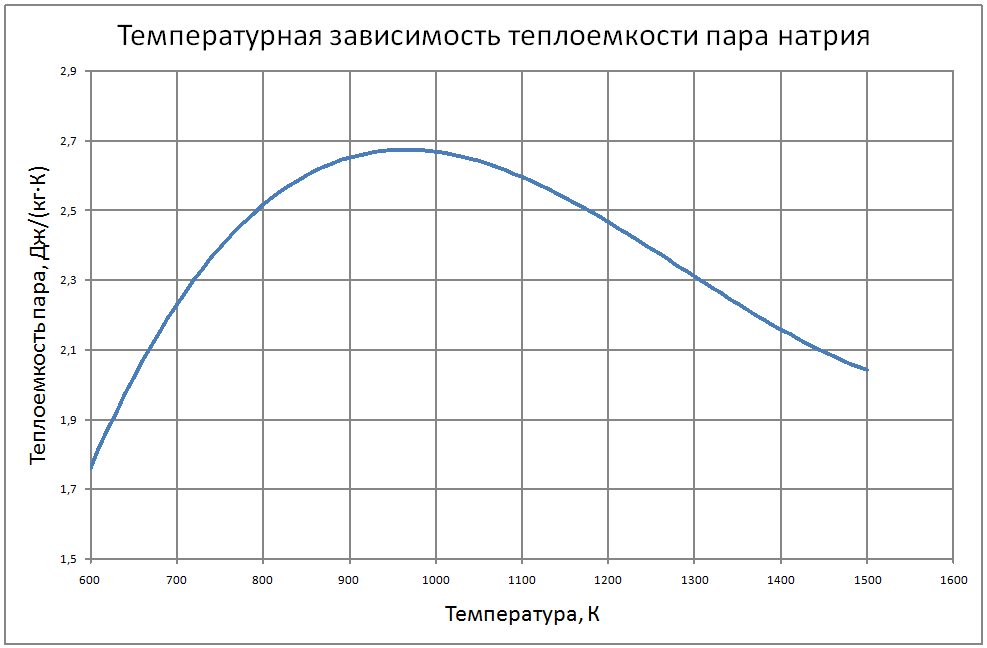
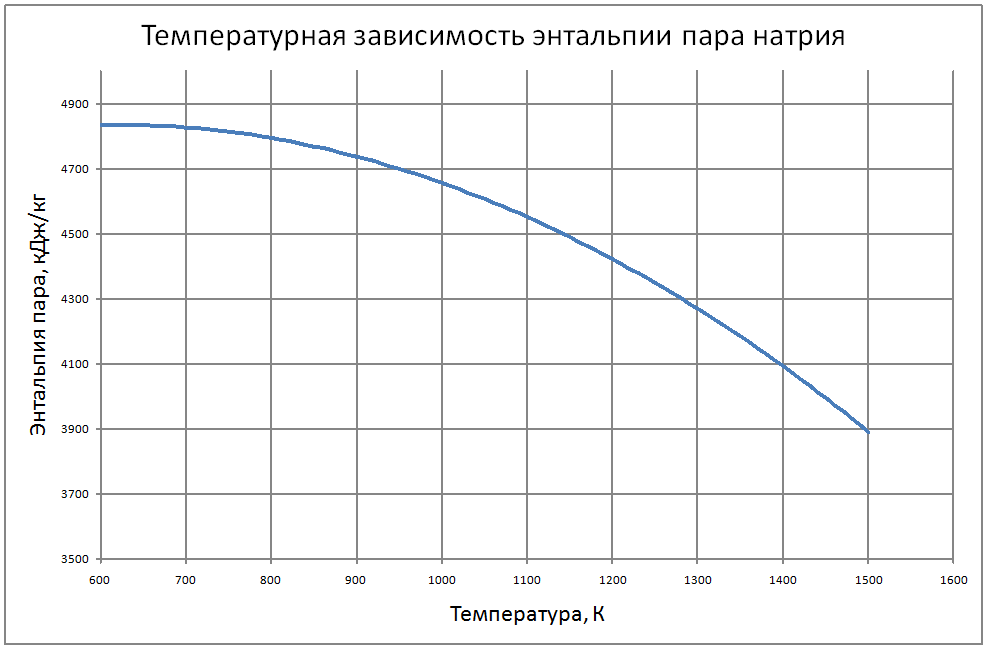
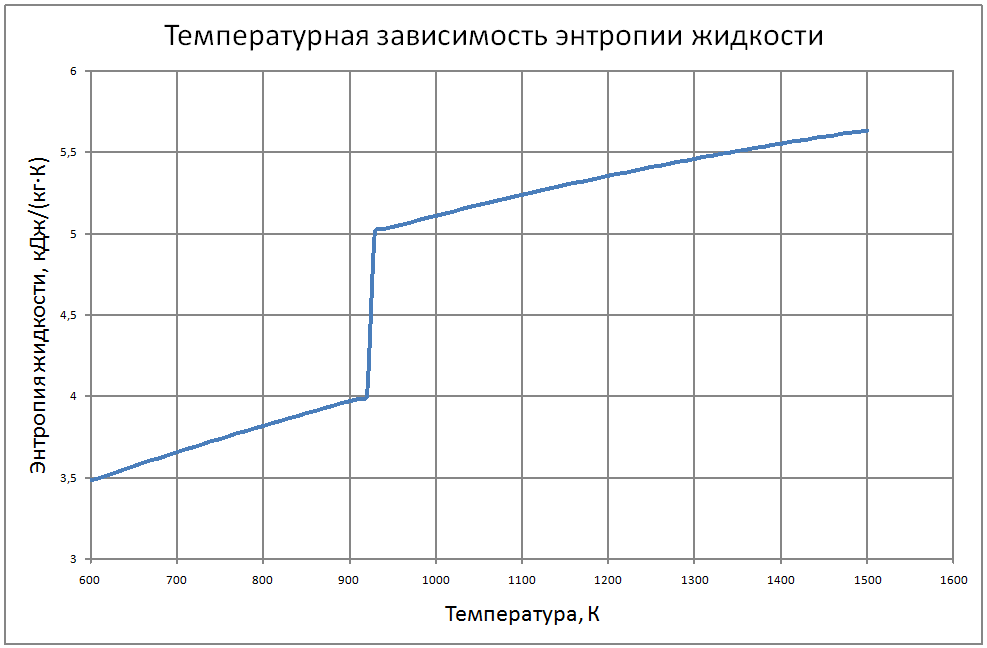
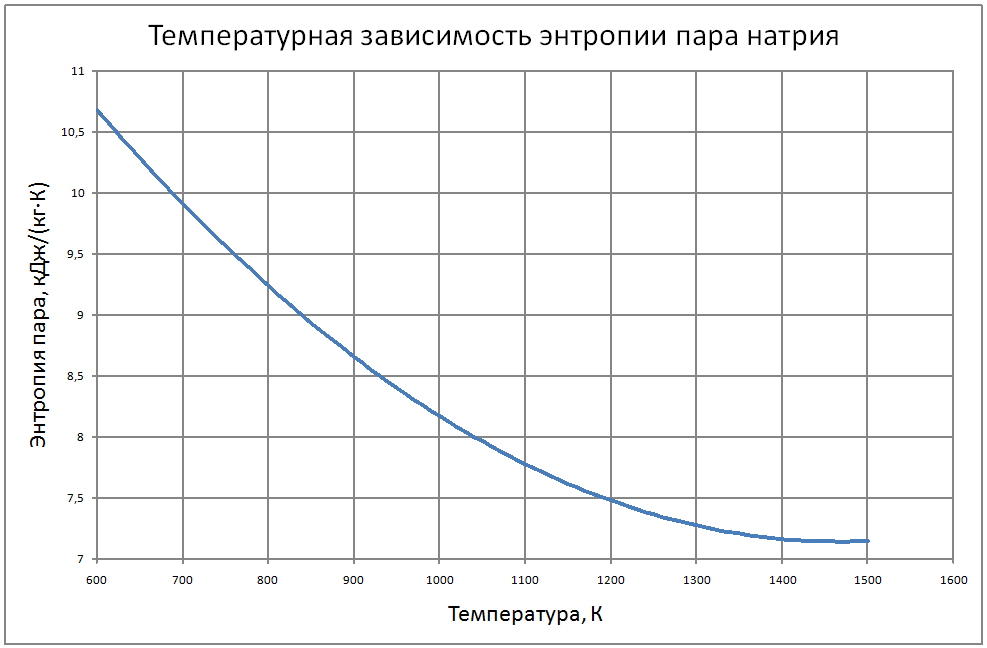
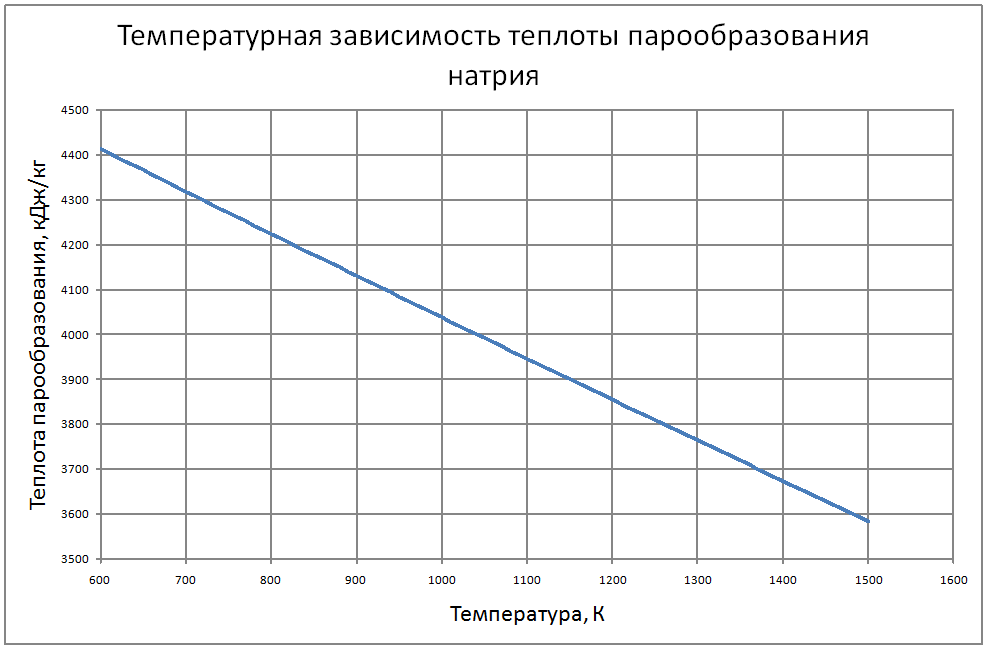
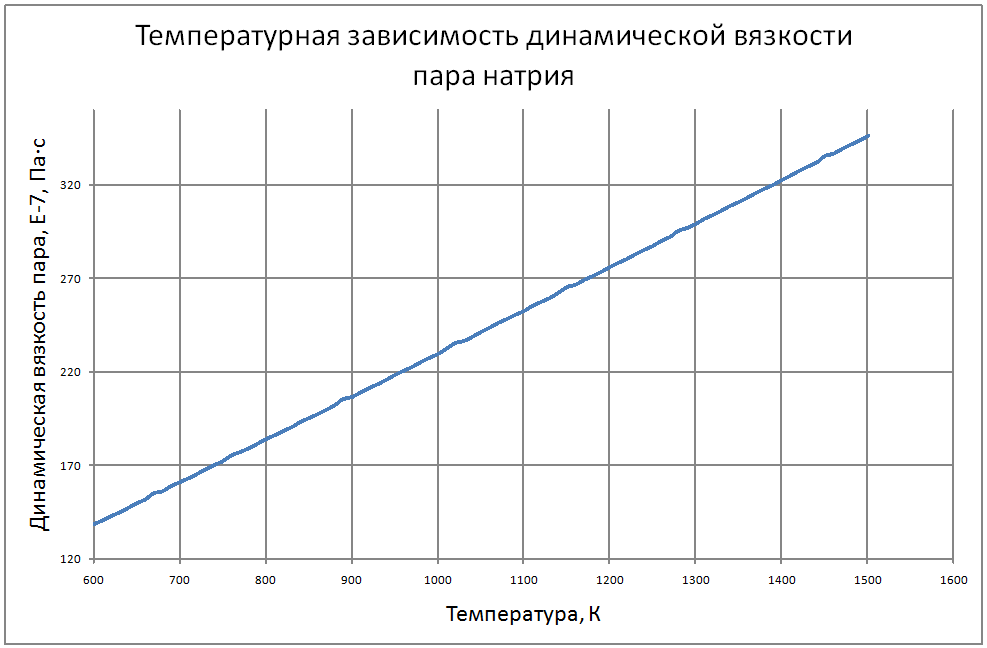
Формулы получены аппроксимацией таблицы 2 из работы [2], погрешность аппроксимации таблиц практически равна нулю, погрешность полученных данных в [2] не приводится. Плотность пара log(ρ"·103) = –15,107+3,447 (T/100) –0,2317 (T/100)2+0,00561 (T/100)3 (11) где ρ" в кг/м3; Т в К. Теплоёмкость пара Cp" = -6,589+0,024T-1,99·10-5T2+5,157·10-5Т3 (12) где Cp" – в кДж/(кг·K); T в K. Энтальпия жидкости и пара: жидкости для интервала температур от 600 К до 1200 К H' (T)-H' (T = 600) = -760+1,27T–3,57·10–6·Т2(13) жидкости для интервала температур от 1300 К до 1500 К H' (T)-H' (T = 600) = -559+1,33T (14) где H' в кДж/кг; Т в К. Энтальпия пара для интервала температур от 600 К до 1500 К H"(T) -H"(T = 600) = -537+1,47T-0,0012Т2+4,1·10-7Т3 (15) Энтропия жидкости и пара Энтропия жидкости для интервала температур от 600 К до 1500 К S'(T) -S'(T = 600) = –1,27+0,0025T-5,8·10-7T2 (16) где S' в кДж/(кг·K); Т в К. Энтропия пара для интервала температур от 600 К до 1500 К S"(T) -S"(T = 600) = 6,45-0,0138·T+4,7·10-6·T2 (17) где S в кДж/(кг·K); Т в К. Теплота парообразования R = 4997-0,993T+3,41·10-5T2 (18) где R в кДж/кг; Т в К. Теплопроводность пара λ" = (-37,64+0,118 T-3,63·10-5T2)·10-3 (19) где λ" в Вт/(м·К); Т в К. Динамическая вязкость пара μ" = (3,95+0,221T+4,76·10-6T2) ·10-7 (20) где μ" в Па·с; Т в К. Кинематическая вязкость, число Прандтля Кинематическая вязкость и число Прандтля рассчитываются по соотношениям: v = μ/ρ, Pr = v/ a (21) В таблице ниже приведены табулированные значения свойств на линии насыщения. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Описана методика расчета термодинамических функций на основе групповых разложений с использованием полученного ранее полуэмпирического уравнения состояния. Погрешность результатов подсчитывается как сумма перенесенной погрешности исходных экспериментальных данных и систематической ошибки от неучета старших групповых интегралов, возникающей при экстраполяции уравнения состояния в область высоких плотностей. Выполнено сравнение результатов расчета с экспериментальными данными о теплоемкости и скорости звука в парах калия, которые не использовались при построении уравнения состояния, а также с расчетными данными других авторов. Приведены таблицы термодинамических свойств паров натрия и калия и погрешностей этих величин при температурах 800 - 2000 К и давлениях 0,01 - 5 МПа. Оценки термодинамических функций и их погрешностей. В [55] построены полуэмпирические уравнения состояния паров натрия и калия в виде разложений давления p и мольной плотности ρ по степеням активности ζ исходных атомов
В [56] проанализированы полученные в результате оценки групповых интегралов bj(T). Групповые разложения других термодинамических функций, аналогичные (1), (2), - энтальпии h, энтропии s, обратной изотермической сжимаемости (∂p/∂ρ)T, термического коэффициента давления (∂p/∂T)ρ, изохорной cv и изобарной cp теплоемкостей, адиабатной скорости звука a = [(cp/cv) (∂p/∂γ)T]½ приведены в [55, 57] и содержат групповые интегралы, а также их первые и вторые производные по температуре. Таким образом, используя найденные в [55] оценки параметров â1, ..., âm, определяющих температурные зависимости групповых интегралов, можно оценить значения любых представляющих интерес термодинамических функций рассматриваемых веществ, хотя для построения уравнения состояния потребовались лишь данные о плотности этих веществ и о потенциалах межатомного взаимодействия. Чтобы вычислить значение некоторой термодинамической функции g при заданных Т и р на основе ее группового разложения g = φ(T,ζ), решаем при этих Т и p уравнение (1) относительно ζ) (численно) и подставляем его корень ζ(T,p) в требуемое групповое разложение: g(T, р) = φ[T, ζ(T,p)]. Уровень значимости предсказываемых таким способом термодинамических функций оценивался путем вычисления по правилу переноса ошибок среднеквадратичных отклонений Δидg, обусловленных погрешностью исходных данных, при использовании с этой целью рассчитанной в [55] ковариационной матрицы оценок параметров covij(â)
Поскольку термодинамические функции зависят от параметров â1, ..., âm как непосредственно (через групповые интегралы и их производные), так и косвенно (через активность), формулы для вычисления величин (3) очень громоздки и здесь не приводятся: они подробно выписаны в [58]. Погрешности стандартных термодинамических функций одноатомных паров Na и К, затабулированных в [59] и аппроксимированных авторами предлагаемой работы, пренебрежимо малы по сравнению с (3). Так как полученное полуэмпирическое уравнение состояния теоретически обосновано, рассчитанные на его основе значения термодинамических функций не содержат каких-либо дополнительных погрешностей, помимо перенесенной погрешности исходных экспериментальных данных (3), в том числе, вообще говоря, и при температурах и давлениях, выходящих за пределы области параметров состояния, в которой располагаются исходные данные (T < 1700 К, p < 3 МПа). Однако при значительном удалении от этой области в сторону высоких плотностей появляется дополнительная систематическая погрешность, вызванная отсутствием в уравнении состояния (1), (2) членов, содержащих пятый и старшие групповые интегралы, которые, как указано в [55, 2], невозможно оценить по имеющимся экспериментальным данным. Хорошо обоснованного способа оценки a priori величин bj(T) при j ≥ 5 для паров Na и К в настоящее время, насколько нам известно, не существует. Поэтому ниже предлагается заведомо грубый экстраполяционный способ оценки указанных величин. Эти величины затем используются для расчета возможного вклада в термодинамические функции g от неучтенной суммы старших членов группового разложения Δэg который целиком рассматривается как дополнительная погрешность расчета в «области экстраполяции». Экстраполяционный расчет термодинамических функций основан на асимптотических оценках групповых интегралов [60], подтверждающихся результатами [55]. bj ~ exp[E(j/2)De/kT] (4) (Е(х)- целая часть х). С учетом (4) разделены вклады четных и нечетных членов ряда (1) p = pнеч + pчет (5) и предполагается, что каждое из слагаемых в правой части (5) можно приближенно заменить суммой, соответствующей бесконечно убывающей геометрической прогрессии
где γ = b3ζ2 и
где δ = (b4/b2)ζ2. Окончательно
Первые четыре члена разложения (6) по степеням активности ζ полностью совпадают с (1). Последующие члены разложения (6) дают экстраполяционные оценки старших групповых интегралов по b2, b3, b4
Используя термодинамические соотношения большого канонического ансамбля, из (6) нетрудно найти аналогичные «аппроксиманты Паде» групповых разложений и других термодинамических функций. Например,
Оценку систематической погрешности расчета термодинамической функции g от неучета старших членов группового разложения Δэg найдем, вычитая из величины gэ(T,р), вычисленной по (6), (8), значение g(T,р), полученное на основе четырехчленного полуэмпирического уравнения состояния (1), (2),
Однако, по-видимому, эта оценка несколько завышена: как показали расчеты, величина (9) сравнивается с (3) уже при p ≈ 1 МПа, в то время как на самом деле групповые интегралы старше четвертого не могут быть оценены по исходным экспериментальным данным, следовательно, их вклад меньше (3) вплоть до р ≤ 2,5 МПа. Поэтому погрешность результатов расчета термодинамических функций при р ? 3 МПа полагалась равной утроенной (в соответствии с правилом «трех сигм») величине (3), а систематическая погрешность (9) дополнительно учитывалась лишь при p > 3 МПа, т. е. в «области экстраполяции»
Сравнение результатов расчета с литературными данными. В первую очередь такое сравнение полезно провести с экспериментальными данными о плотности [61], изобарной теплоемкости [62] и адиабатной скорости звука [63] пара калия, которые при построении уравнения состояния не использовались. Соответствующие материалы представлены в табл. 1 - 3. Таблица 1. Сравнение результатов расчета плотности пара калия с экспериментальными данными [61]
Таблица 2. Сравнение результатов расчета изобарной теплоемкости пара калия с экспериментальными данными [62]
Таблица 3. Сравнение результатов расчета адиабатной скорости звука пара калия с экспериментальными данными [63]
Совпадение наших расчетов плотности пара калия с результатами измерений [61] свидетельствует не только о точности полуэмпирического уравнения состояния, но и о его экстраполяционных возможностях, поскольку данные [61] частично лежат в области параметров состояния, значительно выходящей за пределы температур и давлений, в которых это уравнение получено. Можно констатировать хорошее согласие нашего расчета с данными [62] о теплоемкости, имеющими, по оценке авторов, погрешность 3 %: расхождения носят случайный характер и укладываются в суммарную погрешность расчета и эксперимента. В то же время результаты нашего расчета систематически (в среднем на 1,5 %) занижены по отношению к данным [63] о скорости звука, погрешность которых, по оценке автора, менее 0,5 %. Такие расхождения заметно превышают суммарную погрешность расчета и эксперимента (0,7 - 0,9 %), и их причина пока не ясна. Впрочем, сами по себе эти расхождения не столь уж велики, и в целом результаты сравнения полуэмпирического уравнения состояния с экспериментом можно признать удовлетворительными. Сопоставим далее наши данные с результатами расчетов термодинамических свойств паров Na и К, выполненных ранее (критический обзор на эту тему приведен в [55]). Относительные отклонения от рассчитанных нами значений - средние (верхняя цифра соответствующей колонки в данной графе) и максимальные (нижняя цифра) - приведены в табл. 4. Таблица 4. Относительные отклонения результатов расчетов термодинамических функций паров натрия и калия (литературные данные) от данных, авторов (в %)
Результаты расчета плотности γ = Mρ по интерполяционным «псевдовириальным» уравнениям состояния [63, 64], как и следовало ожидать, отклоняются от наших данных в пределах утроенного среднеквадратичного отклонения исходных данных. Наилучшее совпадение имеет место для энтропии - термодинамической функции, наименее чувствительной к нюансам поведения уравнения состояния. Зато очень велики отличия в значениях изобарной теплоемкости, причем их знак в работах [63, 64] противоположен. Такие расхождения, несомненно, свидетельствуют о том, что «псевдовириальные коэффициенты» [56], использованные в [63, 64], заметно и притом незакономерным образом искажают характер кривизны термодинамической поверхности, к которой особенно чувствительна теплоемкость. Плотность пара натрия, рассчитанная в [65], превосходно согласуется с нашими данными во всем охваченном в [65] диапазоне параметров (1000 - 1600 К, 0,01 - 1 МПа), что объясняется близостью констант равновесия «квазихимического» уравнения состояния [65] нашим групповым интегралам [56]. К сожалению, отличия по другим термодинамическим; функциям выходят за границы разумного: так, при 1500 К и 0,01 МПа, когда не только неидеальность, но и образование димеров практически не оказывают влияния на термодинамическое поведение пара натрия, расхождение в энтропии составляет 1,5 %. По-видимому, в [65] приняты ошибочные стандартные термодинамические функции одноатомного пара Na, что, конечно, весьма удивительно. Значительные расхождения наших результатов с данными справочника [66] вызваны в основном неправдоподобно большими значениями принятого там второго вириального коэффициента, учитывающего поправку на неидеальность за счет взаимодействия мономеров [55]. В случае калия- эта ошибка частично компенсируется неточностью принятого в [66] значения энергии диссоциации димера К2. Как видно из последней графы табл. 4, значения термодинамических функций, рассчитанные в [66] в идеально-газовом приближении, ближе к действительности, чем с учетом неидеальности. Уже после того, как эта работа была сдана в печать, появился обзор [67], в котором на основе экспериментальных данных о плотности, указанных в [55], получены интерполяционные уравнения состояния пара натрия при 960 ≤ T ≤ 1700 К, 0,01 ≤ p ≤ 2,5 МПа и калия при 840 ≤ T ≤ 1700 К, 0,01 ≤ p ≤ 2,5 МПа, имеющие вид «псевдовириального» разложения давления по степеням плотности до четвертой включительно, и на их основе рассчитаны таблицы термодинамических свойств. Расхождения с результатами настоящей работы таковы: для натрия по плотности не более 0,4 %, по энтальпии и энтропии - менее 0,5 %, по скорости звука - до 1 %, по теплоемкости сp - до 5 %; для калия по плотности до 1 % при низких температурах и давлениях и не более 0,5 % при повышенных, по энтальпии - не более 0,5 %, по энтропии - менее 0,3 %, по скорости звука - до 2 % при низких температурах и давлениях и не более 0,5 % при повышенных, по теплоемкости сp - до 5 - 10 %, а при самых низких Т и р - до 20 %. Указанные расхождения превышают оцененные погрешности расчета термодинамических функций, причем для скорости звука и особенно теплоемкости - значительно. По-видимому, они вызваны различием в формах уравнения состояния, иным выбором авторами [67] по сравнению с [55] весовых множителей при обработке как разных данных, так и разных серий одного и того же эксперимента, и, наконец, включением в обработку недостаточно надежных низкотемпературных данных о плотности пара калия. В целом проведенный выше анализ позволяет авторам надеяться, что результаты расчета термодинамических свойств паров натрия и калия, полученные в предлагаемой работе, наиболее надежны по сравнению с имеющимися в настоящее время литературными данными. Таблицы термодинамических функций. В табл. 5 приведены результаты расчета безразмерного отношения активности ζ к величине р/RT (поскольку f = ζRT - летучесть, или фугитивность, то указанное отношение представляет собой коэффициент летучести f/p), массовой плотности γ = Mρ (М - атомная масса), энтальпии h, энтропии s и изобарной теплоемкости ср, отношения ср/cv и адиабатной скорости звука а паров натрия и калия. В табл. 6 - погрешности перечисленных величин, рассчитанные по (10). Таблицы охватывают состояния перегретых и (частично) переохлажденных (на 100 -150 К) паров. Величина ζRT/р, как отмечено в [56], может служить оценкой мольной доли мономеров x1. Таблиц 5. Термодинамические свойства пара натрия
Таблиц 6. Погрешности результатов расчета термодинамических свойств пара натрия
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





 (1)
(1) (2)
(2) (3)
(3)

 (6)
(6) (7)
(7)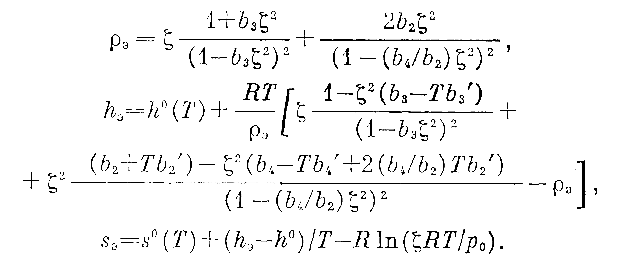 (8)
(8) (9)
(9)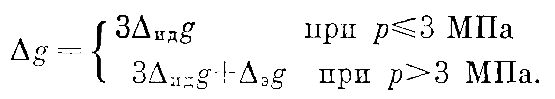 (10)
(10)