База данных по теплофизическим свойствам жидкометаллических теплоносителей перспективных ядерных реакторов
Теплофизические свойства жидкого лития и его пара
ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОМЕТАЛЛИЧЕСКИХ ТЕПЛОНОСИТЕЛЕЙ
Раздел составлен по материалам работ [9 - 15, 40].
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
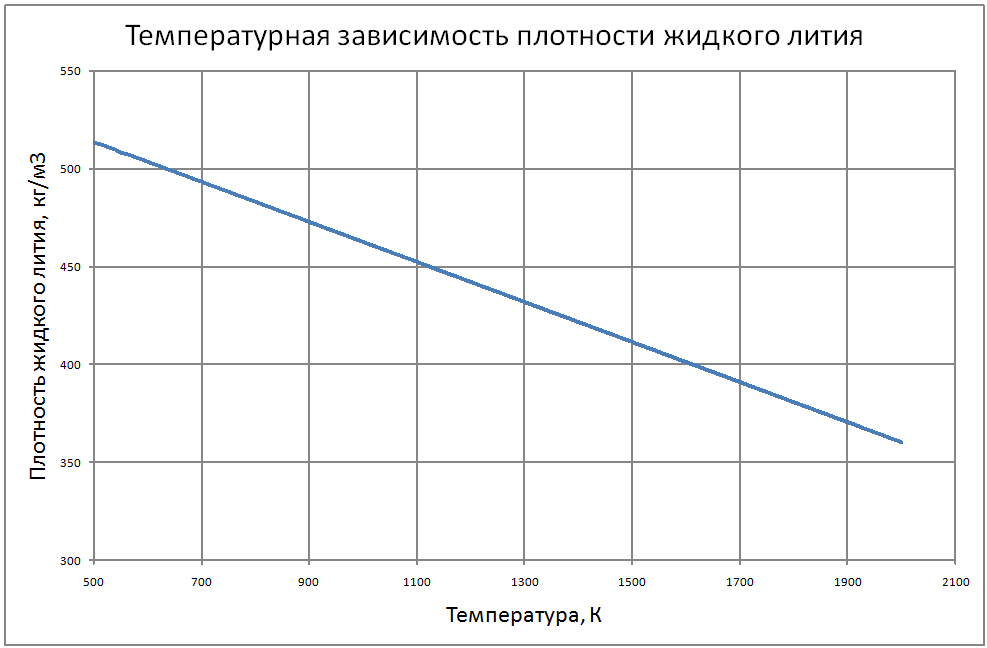
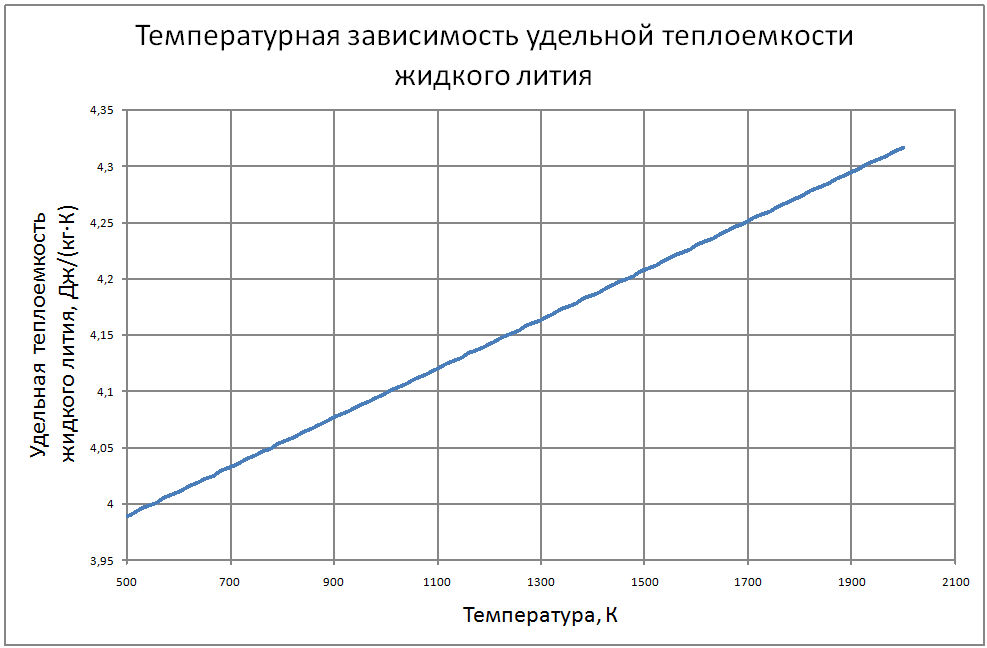
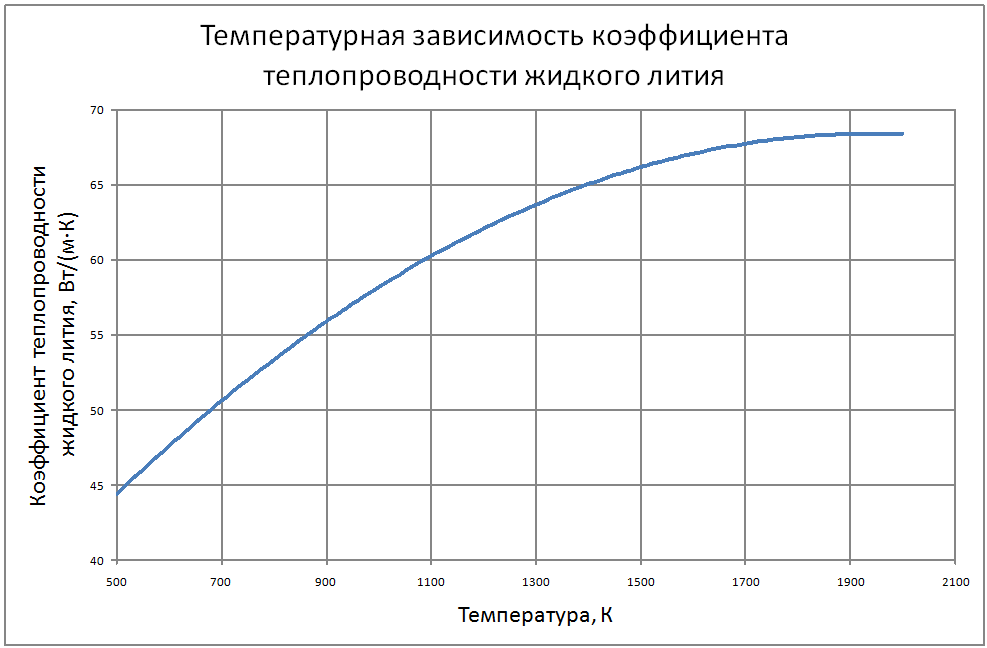
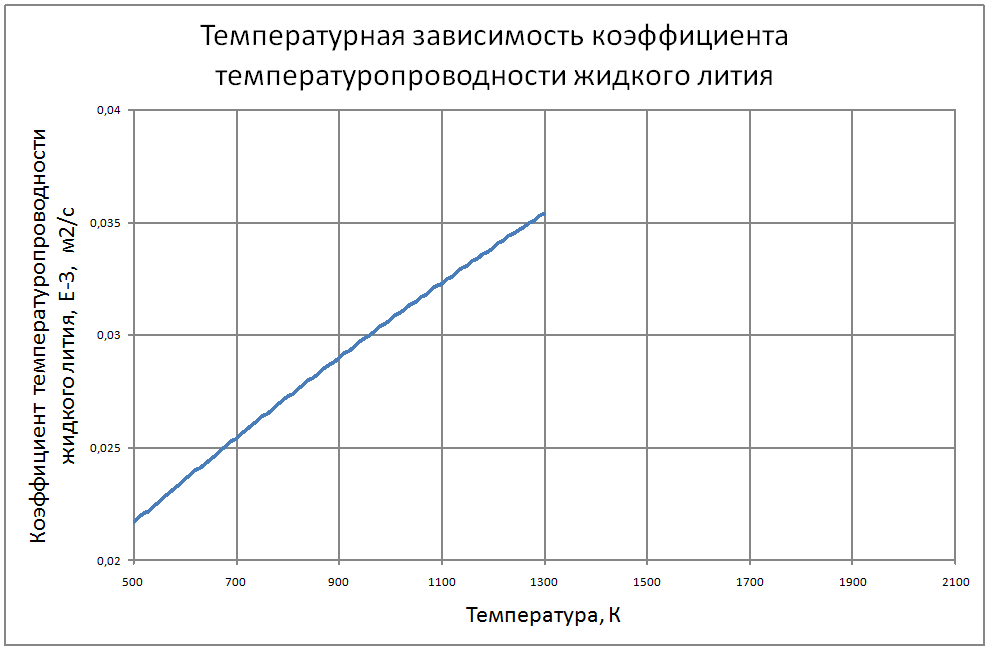
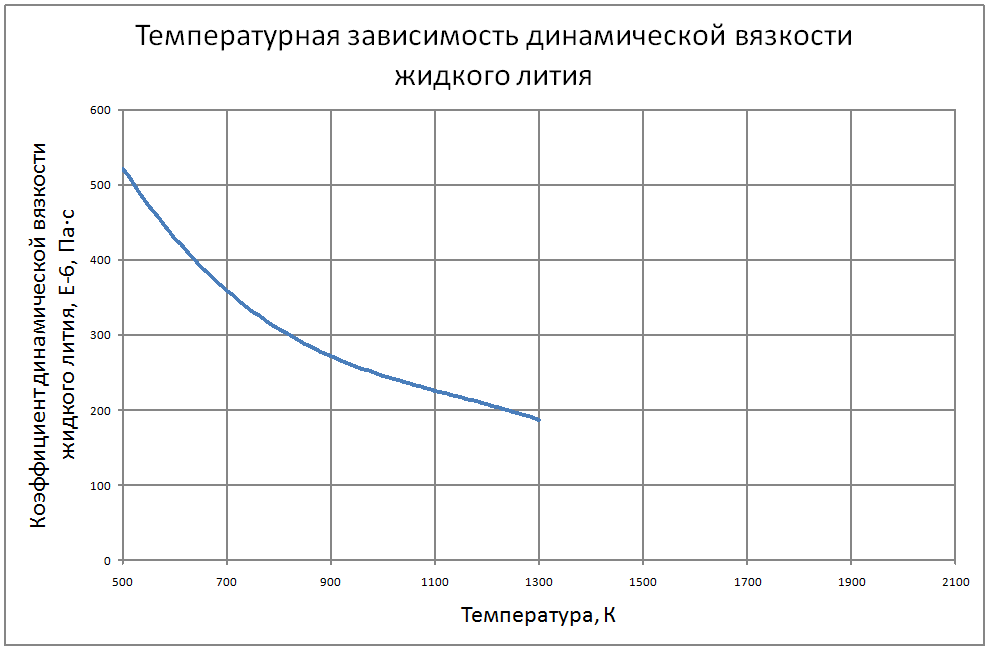
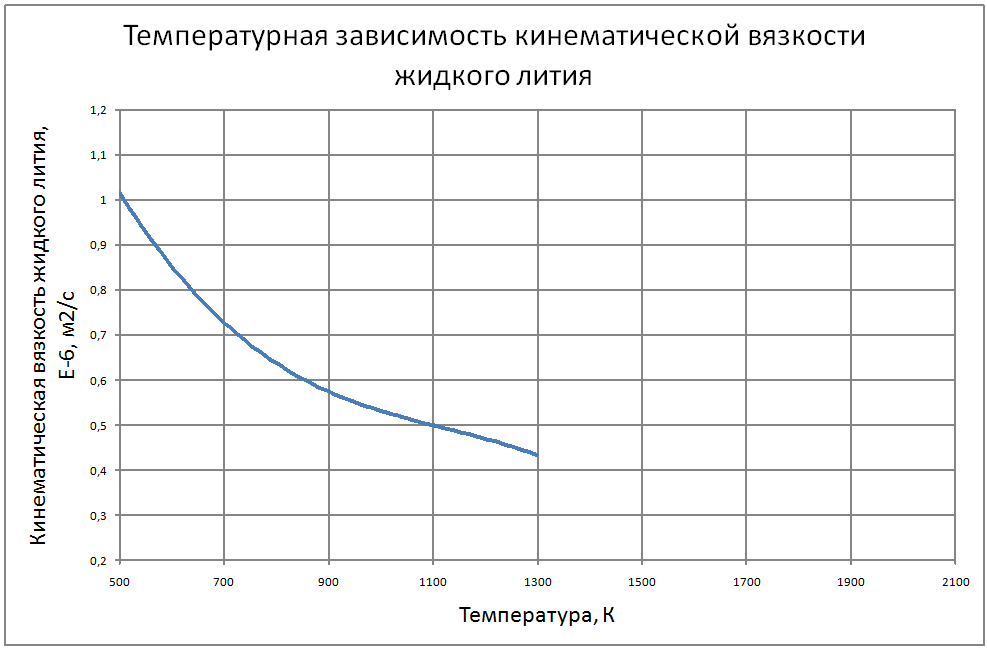
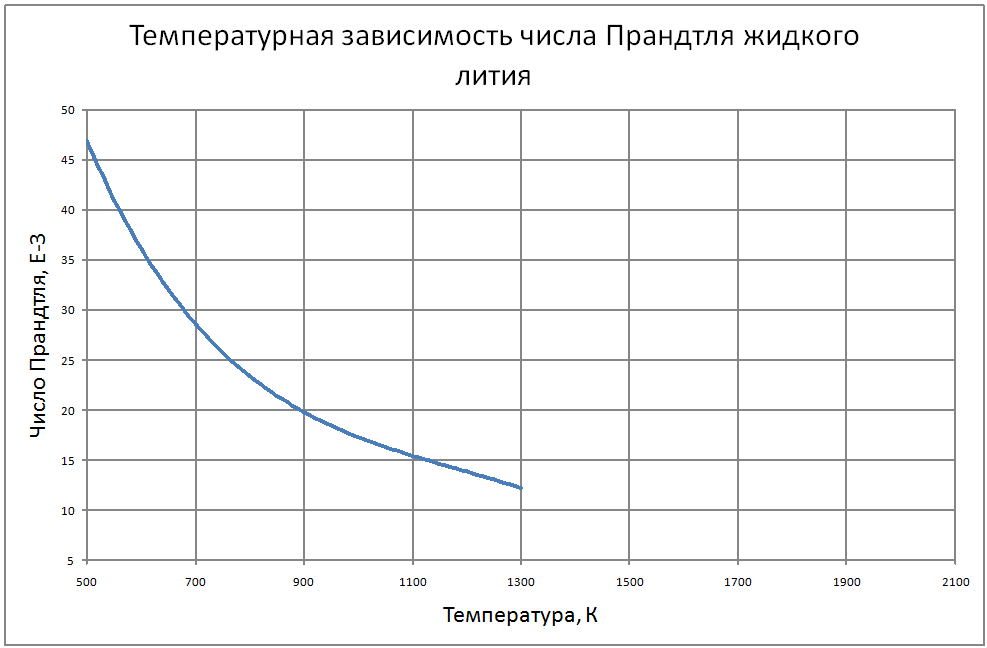
Плотность жидкого лития (массовое содержание различных примесей не более 0.5%) рассчитывается по формуле ρ = 564,64-0,102 ·T. (1) где ρ - кг/м3, T - K. Пределы применимости формулы T от 500 до 1800 K. Погрешность Δ расчета ρ составляет ± 0,3%. Теплоёмкость жидкого лития рассчитывается по формулам, где Cр - кДж/(кг ·К): -при T от 454 до 700 K по формуле Cp = 4,732-7,833·10-4T;(2) - при T от 700 до 1200 K по формуле Cp = 4,243-8,44·10-5T;(3) - при T от 1200 до 2000 K по формуле Cp = 3,88+ 2,185·10-4T, (4) Погрешность Δ расчета Cр: - по формулам (2)-(3) составляет ± 0,3%; - по формуле (4) составляет ± 1%. Коэффициент теплопроводности жидкого лития рассчитывается по формуле: λ = 24,8 + 45,10-3T-11,6·10-6Т2 (5) где λ - Вт/(м·K). Пределы применимости формулы: T от 454 до 1300 K. Погрешность δ расчета λ составляет ± 8%. Коэффициент поверхностного натяжения жидкого лития рассчитывается по формуле: σ = 439 -18,4 10-3T –132,2·10-6T2+37,44·10-9T3,(6) где σ - Н/м. Пределы применимости формулы: T = от 454 до 1300 K. Погрешность Δ расчета σсоставляет ±8%. Коэффициент динамической вязкости жидкого лития рассчитывается по формуле: μ = (1493-2,998Т+2,477·10-3T2-7,258·10-7T3 ,(7) где μ - Па·с. Пределы применимости формулы: T от 454 до 1800 K. Погрешность Δ расчета μ - при T = 454 ÷ 1300 K составляет ± 5%; - при T = 1300 ÷ 1800 K ± 10%. Удельное электросопротивление рассчитывается по формуле: ρe = 10-8 [0,925·109 T-1+2,317·106-0,713·103T]-1, Ом·м. (8) Пределы применимости формулы: t = 100 ÷ 1300 °С. Коэффициент кинематической вязкости жидкого лития v. коэффициент температуропроводности и число Прандтля жидкого лития рассчитывается по известным значениям μ, ρ, λ, Cр : ν = μ/ρ ; a = λ/ρ·Cp; Pr = ν/a (9) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
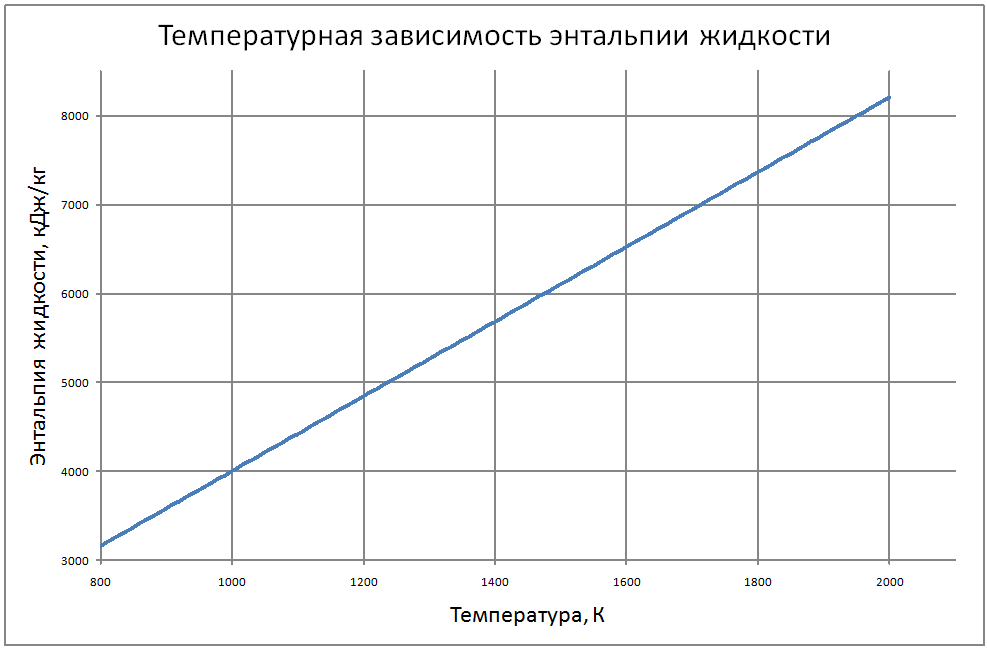
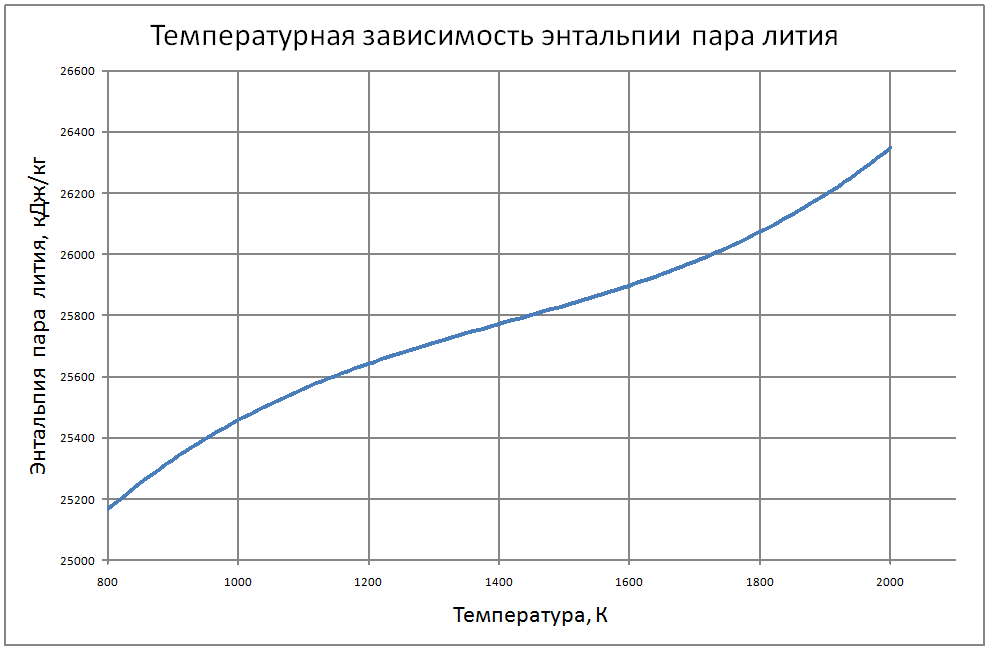
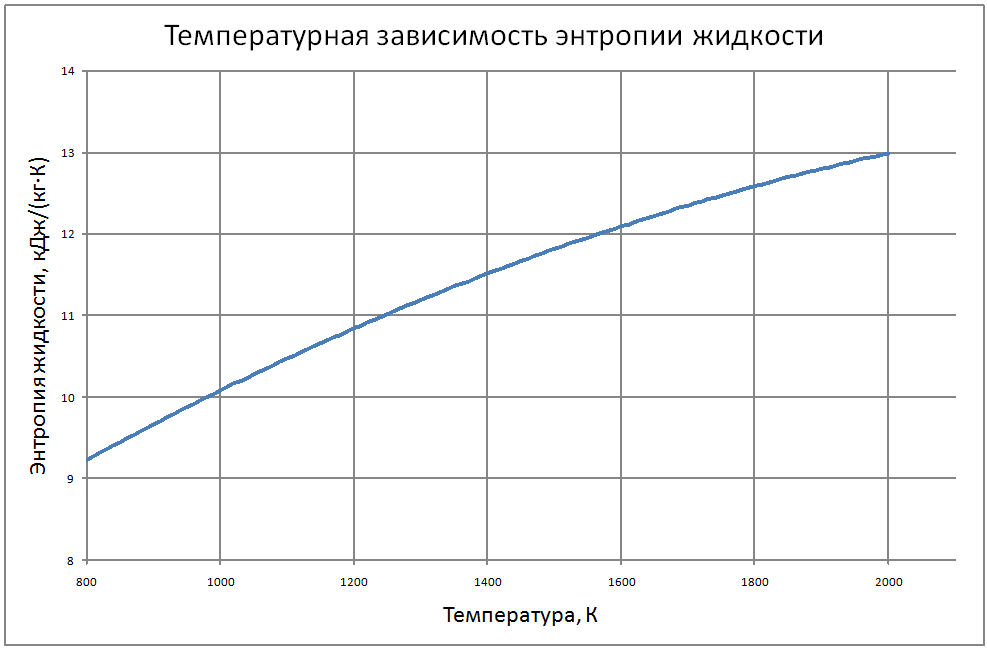
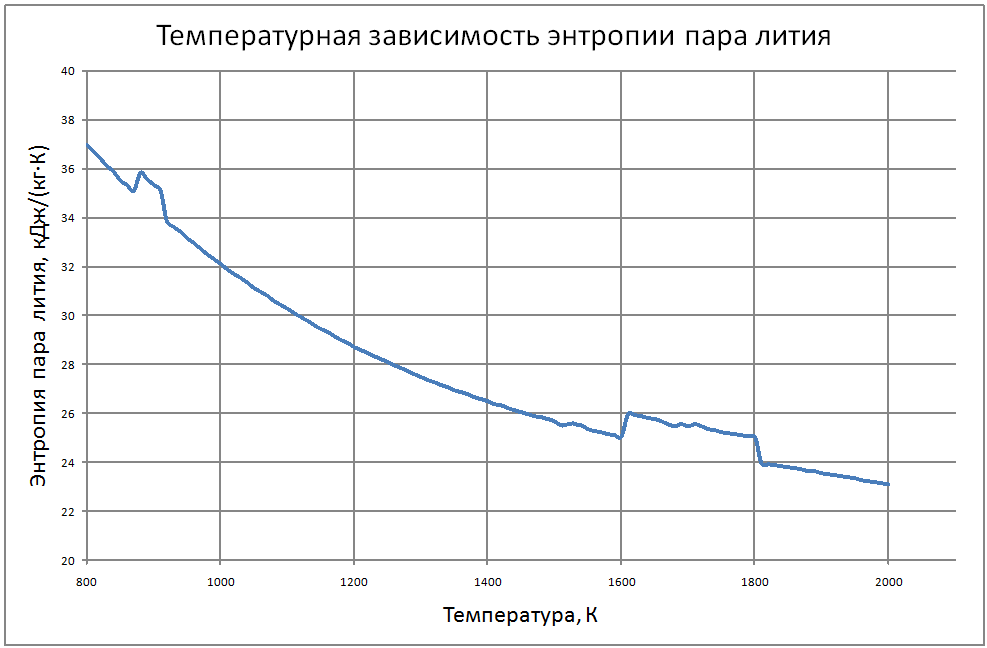
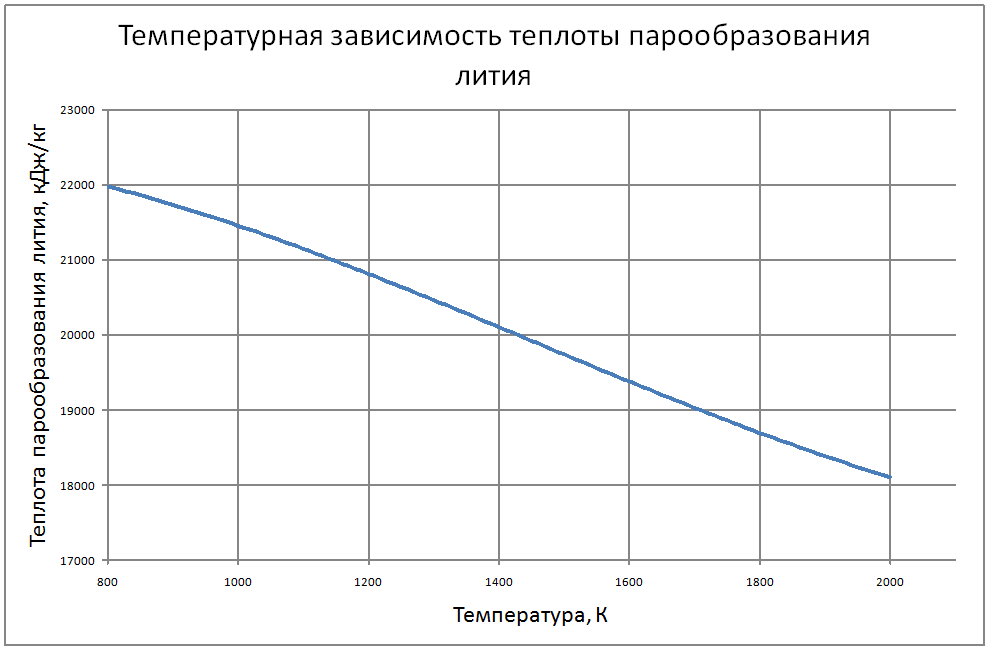
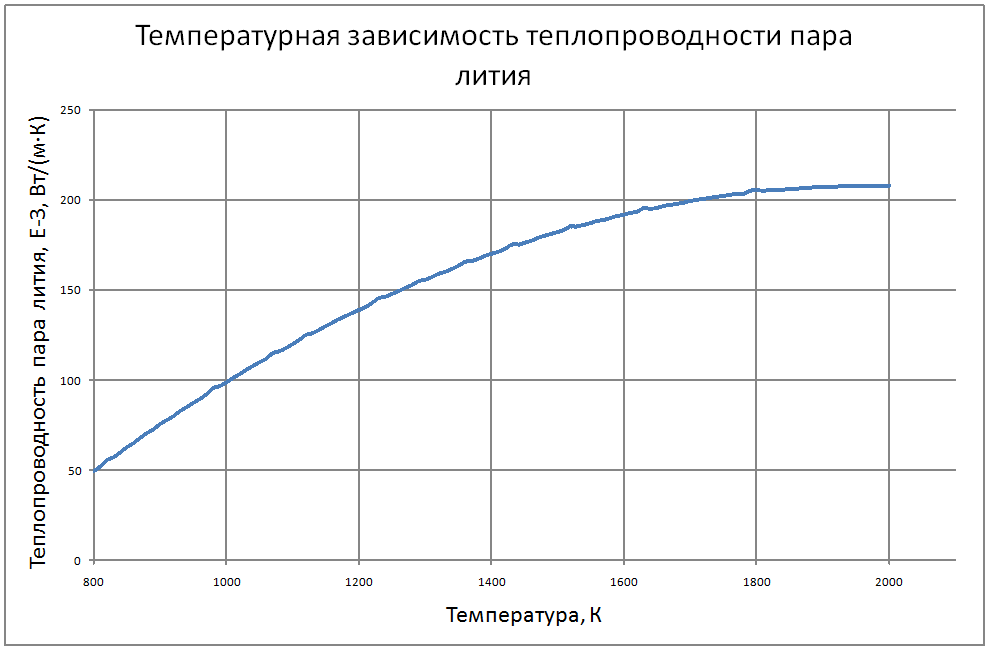
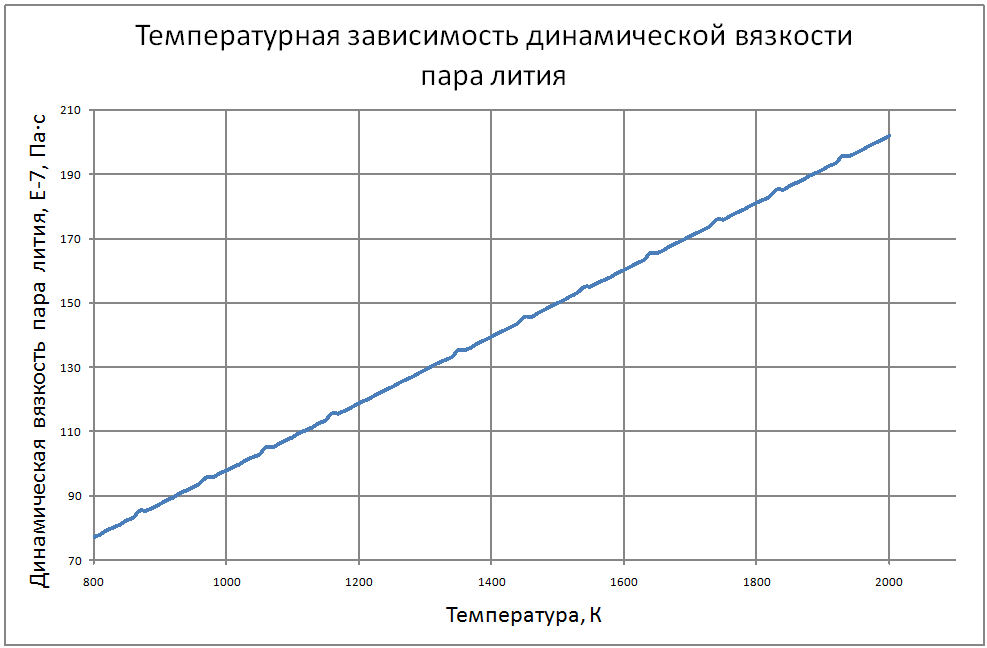
Теплофизические свойства жидкого лития и его пара на линии насыщения (формулы получены по таблице 2 из работы [9, 10], погрешность аппроксимации таблиц практически равна нулю, погрешность полученных данных в [9, 10] не приводится Плотность пара для интервала температур от 1000 К до 1400 К ρ" = (290-1,19T+0,00184T2-1,25·10-6T3+3,23·10-10T4) ·10-3(10) для интервала температур от 1400 К до 2000 К ρ" = (-3388+7,33T-0,00534T2+1,314·10-6T3) ·10-3 (11) где &rho"; в кг/м3; Т в К. Теплоёмкость пара для интервала температур от 800 К до 2000 К: Cp" = -25,5+0,064T-3,71·10-5T2+6,71·10-9T3(12) где Cp" – в кДж/(кг·K); T – K. Энтальпия жидкости для интервала температур от 800 К до 2000 К H' (T)-H' (T = 800) = -3369+4,2T (13) где H' в кДж/кг; Т в К. Энтальпия пара для интервала температур от 800 К до 2000 К H"(T) -H"(T = 800) = -3274+7,07T-0,00458Т2+1,08·10-6Т3 (14) где H" в кДж/кг; Т в К. Энтропия жидкости для интервала температур от 800 К до 2000 К S'(T) -S' (T = 800) = -4,26+0,00628T-1,125·10-6T2 (15) где S' в кДж/(кг·K); Т в К. Энтропия пара для интервала температур от 800 К до 2000 К S"(T) -S"(T = 800) = 41,45-0,079T+4,02·10-5T2-7,23·10-9T3 (16) где S"( в кДж/(кг·K); Т в К. Теплота парообразования для интервала температур от 800 К до 2000 К R = 21764+3,474T-0,0049T2+1,125 10-6T3 (17) где R в кДж/кг; Т в К. Теплопроводность пара для интервала температур от 1100 К до 2000 К λ" = (-240+0,454 T-1,15·10-4T2)·10-3 (18) где λ" в Вт/(м·К); Т в К. Динамическая вязкость пара для интервала температур от 1300 К до 2000 К μ" = (-5,86+0,203T)·10-7 (19) где μ" в Па·с; Т в К. В таблице 2 приведены реперные значения свойств на линии насыщения из [3]. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Методом проникающего γ - излучения измерена плотность лития в конденсированном состоянии в диапазоне от комнатной температуры до ~700 К. Чистота исследованного лития составляла 99.95 мас. %. Доверительная погрешность проведенных экспериментов не превышала 0.3%. По результатам этих измерений рассчитан коэффициент объемного термического расширения лития в широком температурном интервале. Полученные опытные данные о термических свойствах лития в твердой и жидкой фазах сравниваются с имеющимися в литературе. ВВЕДЕНИЕ Легкоплавкие металлы и сплавы с учетом комплекса их ядерно - физических и физико - химических свойств находят широкое применение в различных областях современной науки и новой техники, в частности в атомной и термоядерной энергетике. Так, они могут использоваться в качестве тритий - воспроизводящего материала, жидкометаллического теплоносителя и защиты первой стенки от ионизирующего и теплового излучения в термоядерных реакторах. Причем наиболее перспективными среди них являются литий - свинцовая эвтектика (0.68 мас. % Li и 99.32 мас. % Pb) [69] и литий с природным соотношением своих изотопов 6Li (7.42 мас. %) и 7Li (92.58 мас. %) [70]. Поэтому расчетно - теоретические и экспериментальные исследования их теплофизических характеристик, в первую очередь плотности и термического расширения в твердой и жидкой фазах, имеют важное практическое значение. На первом этапе работы методом просвечивания гамма - квантами были проведены исследования плотности и коэффициента объемного термического расширения (КОТР) литий - свинцового сплава эвтектического состава в конденсированном состоянии в интервале от комнатной температуры до 880 К [71] и жидкого лития в диапазоне от температуры плавления до ~900 К [72]. В продолжение этой работы тем же самым методом была измерена плотность лития в твердой и жидкой фазах в температурном интервале 291 - 686 К. МАТЕРИАЛ И МЕТОД ИССЛЕДОВАНИЯ В экспериментах использовался металлический литий высшей категории качества (марки ЛЭ-1 по ГОСТ 8774-75) с чистотой 99.95 мас. %. Основными примесями в нем были магний, кремний и кальций, общее содержание которых не превышало 0.05 мас. %. Дополнительный химический анализ лития, проведенный после окончания основных измерений в специализированной химико - аналитической лаборатории, показал, что его чистота в процессе экспериментов практически не изменялась. Измерения плотности лития в твердой и жидкой фазах выполнялись методом проникающего гамма - излучения. Эта методика была детально описана ранее в [73] и успешно использовалась для изучения температурной зависимости многих металлов и металлических сплавов в конденсированном состоянии в диапазоне от комнатной температуры до - 2000 К (см., например, [73 - 76]). Методические особенности определения погрешности опытных данных о плотности исследованных веществ, полученных с помощью радиационной методики, приведены в [77]. Здесь же следует отметить, что главные элементы экспериментальной установки, в том числе и измерительная ячейка с рабочим тиглем, изготовлялись из нержавеющей стали марки 12Х18Н10Т, термическое расширение которой принималось по стандартным справочным данным [78]. Температура лития контролировалась хромель - алюмелевой термопарой градуировки К по ГОСТ Р 8.585-2001, дополнительно поверенной по реперным точкам - температурам затвердевания (плавления) индия, свинца и цинка - Международной температурной шкалы 1990 г. (МТШ-90). При этом ее погрешность составляла ±0.1 - 0.2 °С в исследованном интервале температур. В качестве источника γ - квантов применялся изотоп 137Cs, активностью ~ 2.5×1011 Бк, а их приемником - сцинтилляционный детектор с монокристаллом NaJ. Так как плотность лития в конденсированном состоянии исследовалась методом проникающего гамма - излучения в относительном варианте, то для расшифровки первичных измерений необходимо было иметь ее опорное значение при какой - нибудь температуре. Поэтому с использованием литературных справочных данных о массовом коэффициенте ослабления γ - излучения лития была определена его плотность в жидкой фазе при температуре плавления (453.65 К по МТШ-90 [79]). Она оказалась равной 519.0 ± 0.5 кг/м3. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ И ИХ АНАЛИЗ Было проведено три серии измерений плотности лития в конденсированном состоянии в температурном диапазоне от 291 до 686 К: одна при повышении температуры и две при ее понижении (табл. 1). В табл. 1 температура указана по МТШ-90. Доверительная погрешность результатов экспериментов, объединяющая систематическую и случайную составляющие, рассчитывалась по методике [80] и оказалась равной 0.3% для твердого лития и 0.2 - 0.3% для его расплава. Таблица 1. Опытные данные о плотности лития в конденсированном состоянии
Опытные данные каждой серии исследования по отдельности для твердой и жидкой фаз лития обрабатывались методом наименьших квадратов (МНК) аппроксимирующим уравнением вида Y = a0 + alT+a2T2 + ... ( 1 ) где Y - плотность ρ, кг/м3 , или коэффициент объемного термического расширения β, 10-5 1/К, речь о котором пойдет дальше; Т - абсолютная температура по МТШ-90, К. Регрессионно - статистический анализ результатов такой обработки с использованием критерия Фишера [81] показал, что во всех случаях оптимальным является линейное аппроксимирующее уравнение (1), коэффициенты а0, а1 вместе со средней квадратической погрешностью Δа0, Δа1 которого приведены в табл. 2. Причем расхождение между опытными данными различных серий как для твердой, так и для жидкой фаз лития не выходят за пределы вышеуказанной величины доверительной погрешности проведенных измерений. Таблица 2. Коэффициенты аппроксимирующего уравнения (1) для плотности лития в конденсированном состоянии и их средняя квадратическая погрешность
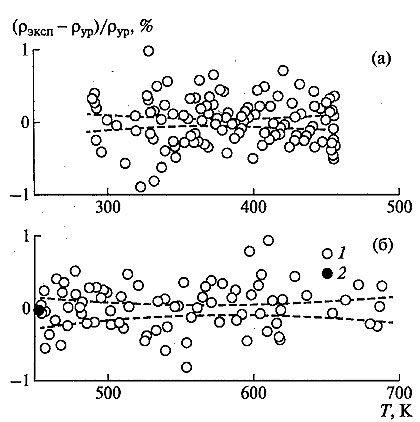
Затем весь массив опытных данных о плотности лития в твердой и жидкой фазах по отдельности обрабатывался МНК аппроксимирующим уравнением (1). Результаты этой обработки приведены в табл. 2. Тогда уравнение (1) можно переписать в несколько другой, более привычной форме: для плотности твердого лития ρтв = 526.87 - 0.06645(T - Tпл), (2) для плотности расплавленного лития ρж = 519.18 - 0.08154(T - Tпл), (3) где первые члены правой части уравнений (2) и (3) представляют собой значения плотности лития в твердой и жидкой фазах при температуре плавления соответственно, а коэффициенты при их вторых членах - температурные коэффициенты плотности (dρ/dT)тв и (dρ/dT)ж лития в исследованных интервалах температур его твердого и жидкого состояний соответственно. Здесь также следует отметить, что полученная таким образом величина плотности расплавленного лития при температуре плавления практически совпадает с ее опорным значением, а сама температура плавления лития (453.5 К), определенная методом проникающего гамма - излучения в процессе проведения основных экспериментов, хорошо согласуется в пределах погрешности температурных измерений с ее справочным значением 453.65 К [79]. Тогда легко найти изменение (скачок) плотности лития при плавлении, играющее важную роль во многих практических приложениях, по формуле Δρ = (ρплтв - ρплж)/ρплтв , (4) где ρплтв, ρплж - плотность твердого и жидкого лития при температуре плавления соответственно. Расчет по формуле (4) дает значение Δρ, равное 1.46 % и мало отличающееся от его рекомендуемой величины 1.57 + 0.20 % [82]. Отклонение опытных данных о плотности лития в конденсированном состоянии от рассчитанных по аппроксимирующему уравнению (1) представлено на рис. 1. Его среднее квадратическое значение не превышало 0.3% для обеих, твердой и жидкой, фаз.
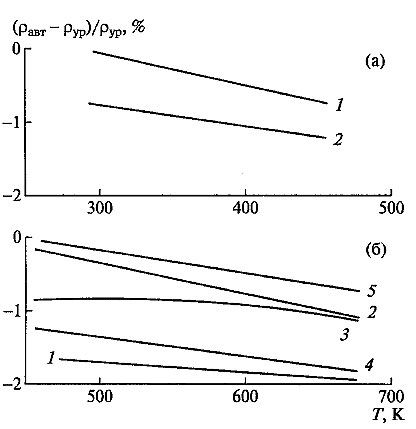
Рис. 1. Отклонение опытных данных настоящей работы о плотности лития в конденсированном состоянии от рассчитанных по аппроксимирующему уравнению (1): (а) - твердая фаза; (б) - жидкая фаза: 1 - экспериментальные точки, 2 - опорная точка, пунктир - границы коридора средней квадратической погрешности расчетных данных о плотности лития в твердой и жидкой фазах с 95 % - ной доверительной вероятностью На рис. 2 показаны расхождения между данными других авторов о плотности лития в твердой и жидкой фазах и результатами проведенных экспериментов. Из него видно, что эти отклонения лежат в пределах заявленной погрешности литературных данных, хотя и имеют отрицательное значение. Последнее обстоятельство объясняется, по-видимому, тем, что измерения в настоящей работе проводились усовершенствованным методом и на образцах лития высокой чистоты. В то же время следует отметить, что новые результаты и опытные данные [72], полученные несколько ранее на той же самой экспериментальной установке и на образцах лития из одной и той же партии металла, хорошо согласуются друг с другом, а отклонение между ними не превышает доверительной погрешности первых (0.3 %).
Рис. 2. Отклонение рекомендуемых справочных данных других авторов о плотности лития в конденсированном состоянии от рассчитанных по аппроксимирующему уравнению (1): (а) - твердая фаза: 1 - данные [83], 2 - [84, 85]; (б) - жидкая фаза: 1 - данные [86], 2 - [83], 3 - [87,88], 4 - [85], 5 - [72]. По полученным опытным данным о плотности лития в конденсированном состоянии рассчитывался его коэффициент объемного термического расширения в твердой и жидкой фазах по формуле β = - (1/ρ)dρ/dT , (5) где dp/dT - температурный коэффициент плотности лития в исследованном температурном диапазоне, речь о котором шла выше. Расчет КОТР по формуле (5) проводился в интервале от комнатной температуры до 700 К с шагом 10 К. Погрешность этих данных оценивалась равной 4% для твердой фазы лития и 3 - 4 % для его расплавленного состояния. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПЛОТНОСТИ Полученные расчетные данные о КОТР лития обрабатывались по отдельности для каждой из исследованных фаз МНК аппроксимирующим уравнением (1). Были найдены следующие температурные зависимости для КОТР лития в диапазоне 273.15 - 700 К: для твердой фазы
для жидкой фазы
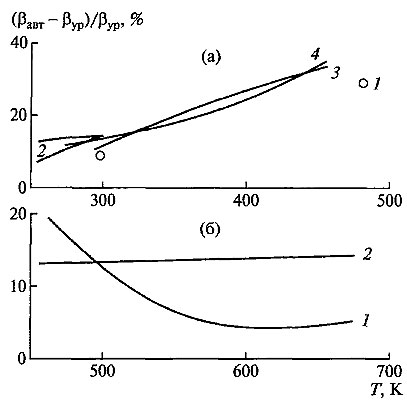
где размерность β - 1/К и T - К. На рис. 3 приведены отклонения рекомендуемых справочных данных о КОТР лития в конденсированном состоянии от рассчитанных по уравнениям (6) и (7) для твердой и жидкой фаз соответственно. Видно, что расхождения между ними не выходят за границы погрешностей литературных данных. Рис. 3. Отклонение рекомендуемых справочных данных других авторов о КОТР лития в конденсированном состоянии от рассчитанных по аппроксимирующему уравнению (1): (а) - твердая фаза: 1 - данные [86], 2 - [89], 3 - [90], 4 - [84, 85]; (б) - жидкая фаза: 1 - данные [87], 2 - [85]. ЗАКЛЮЧЕНИЕ На образцах лития высокой чистоты проведены надежные измерения его плотности в конденсированном состоянии при технически важных температурах. Результаты выполненных экспериментов в значительной степени расширяют массив опытных данных о плотности твердого и жидкого лития, что позволяет в дальнейшем сделать их совместную обработку весовым методом наименьших квадратов и получить стандартные справочные данные о плотности и КОТР лития в широком температурном диапазоне. Работа выполнена при финансовой поддержке РФФИ (проект № 09-08-00254). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||